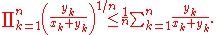Mahler's inequality
Encyclopedia
In mathematics
, Mahler's inequality states that the geometric mean
of the term-by-term sum of two finite sequences of positive numbers is greater than or equal to the sum of their two separate geometric means:
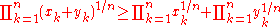
when xk, yk > 0 for all k.
The inequality was named after Kurt Mahler
.
, we have:
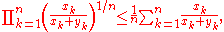
and
Hence,
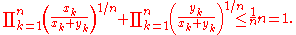
Clearing denominators then gives the desired result.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Mahler's inequality states that the geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
of the term-by-term sum of two finite sequences of positive numbers is greater than or equal to the sum of their two separate geometric means:
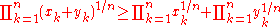
when xk, yk > 0 for all k.
The inequality was named after Kurt Mahler
Kurt Mahler
Kurt Mahler was a mathematician and Fellow of the Royal Society.He was a student at the universities in Frankfurt and Göttingen, graduating with a Ph.D...
.
Proof
By the inequality of arithmetic and geometric meansInequality of arithmetic and geometric means
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if...
, we have:
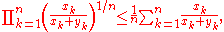
and
Hence,
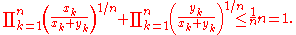
Clearing denominators then gives the desired result.