
Malliavin's absolute continuity lemma
Encyclopedia
In mathematics
— specifically, in measure theory — Malliavin's absolute continuity lemma is a result due to the French
mathematician
Paul Malliavin
that plays a foundational rôle in the regularity (smoothness
) theorem
s of the Malliavin calculus
. Malliavin's lemma gives a sufficient condition for a finite Borel measure to be absolutely continuous
with respect to Lebesgue measure
.
al Euclidean space
Rn. Suppose that, for every x ∈ Rn, there exists a constant C = C(x) such that
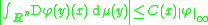
for every C∞ function φ : Rn → R with compact support. Then μ is absolutely continuous with respect to n-dimensional Lebesgue measure λn on Rn. In the above, Dφ(y) denotes the Fréchet derivative
of φ at y and ||φ||∞ denotes the supremum norm of φ.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— specifically, in measure theory — Malliavin's absolute continuity lemma is a result due to the French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Paul Malliavin
Paul Malliavin
Paul Malliavin was a French mathematician. He was Professor Emeritus at the Pierre and Marie Curie University. He was a member of the Academy of Sciences since 1979.-Domains of research:...
that plays a foundational rôle in the regularity (smoothness
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
) theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s of the Malliavin calculus
Malliavin calculus
The Malliavin calculus, named after Paul Malliavin, is a theory of variational stochastic calculus. In other words it provides the mechanics to compute derivatives of random variables....
. Malliavin's lemma gives a sufficient condition for a finite Borel measure to be absolutely continuous
Absolute continuity
In mathematics, the relationship between the two central operations of calculus, differentiation and integration, stated by fundamental theorem of calculus in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration and absolute continuity...
with respect to Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
.
Statement of the lemma
Let μ be a finite Borel measure on n-dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn. Suppose that, for every x ∈ Rn, there exists a constant C = C(x) such that
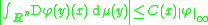
for every C∞ function φ : Rn → R with compact support. Then μ is absolutely continuous with respect to n-dimensional Lebesgue measure λn on Rn. In the above, Dφ(y) denotes the Fréchet derivative
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
of φ at y and ||φ||∞ denotes the supremum norm of φ.

