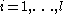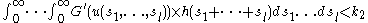Massera's lemma
Encyclopedia
In stability theory
and nonlinear control
, Massera's lemma, named after José Luis Massera
, deals with the construction of the Lyapunov function
to prove the stability of a dynamical system
. The lemma appears in as the first lemma in section 12, and in more general form in as lemma 2. In 2004, Massera's original lemma for single variable functions was extended to the multivariable case, and the resulting lemma was used to prove the stability of switched dynamical systems, where a common Lyapunov function describes the stability of multiple modes and switching signals.
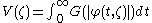
for an asymptotically stable dynamical system whose stable trajectory starting from
The lemma states:
Stability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
and nonlinear control
Nonlinear control
Nonlinear control is the area of control engineering specifically involved with systems that are nonlinear, time-variant, or both. Many well-established analysis and design techniques exist for LTI systems ; however, one or both of the controller and the system under control in a general control...
, Massera's lemma, named after José Luis Massera
José Luis Massera
José Luis Massera was an Uruguayan mathematician who researched the stability of differential equations....
, deals with the construction of the Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
to prove the stability of a dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
. The lemma appears in as the first lemma in section 12, and in more general form in as lemma 2. In 2004, Massera's original lemma for single variable functions was extended to the multivariable case, and the resulting lemma was used to prove the stability of switched dynamical systems, where a common Lyapunov function describes the stability of multiple modes and switching signals.
Massera's original lemma
Massera’s lemma is used in the construction of a converse Lyapunov function of the following form (also known as the integral construction)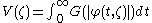
for an asymptotically stable dynamical system whose stable trajectory starting from

The lemma states:
Letbe a positive, continuous, strictly decreasing function with
as
. Let
be a positive, continuous, nondecreasing function. Then there exists a function
such that
and its derivative
are class-K functions defined for all t ≥ 0
- There exist positive constants k1, k2, such that for any continuous function u satisfying 0 ≤ u(t) ≤ g(t) for all t ≥ 0,
Extension to multivariable functions
Massera's lemma for single variable functions was extended to the multivariable case by Vu and Liberzon.
Letbe a positive, continuous, strictly decreasing function with
as
. Let
be a positive, continuous, nondecreasing function. Then there exists a differentiable function
such that
and its derivative
are class-K functions on
.
- For every positive integer
, there exist positive constants k1, k2, such that for any continuous function
satisfying
for all
,
we have