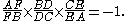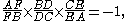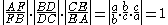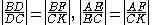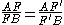Menelaus' theorem
Encyclopedia
Menelaus of Alexandria
Menelaus of Alexandria was a Greek mathematician and astronomer, the first to recognize geodesics on a curved surface as natural analogs of straight lines.-Life and Works:...
, is a theorem about triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s in plane geometry
Plane geometry
In mathematics, plane geometry may refer to:*Euclidean plane geometry, the geometry of plane figures,*geometry of a plane,or sometimes:*geometry of a projective plane, most commonly the real projective plane but possibly the complex projective plane, Fano plane or others;*geometry of the hyperbolic...
. Given a triangle ABC, and a transversal
Transversal (geometry)
In geometry, a transversal is a line that passes through two or more other lines in the same plane at different points. When the lines are parallel, as is often the case, a transversal produces several congruent and several supplementary angles...
line that crosses BC, AC and AB at points D, E and F respectively, with D, E, and F distinct from A, B and C, then
This equation uses signed lengths of segments, in other words the length AB is taken to be positive or negative according to whether A is to the left or right of B in some fixed orientation of the line. For example, AF/FB is defined as having positive value when F is between A and B and negative otherwise.
The converse is also true: If points D, E and F are chosen on BC, AC and AB respectively so that
then D, E and F are collinear. The converse is often included as part of the theorem.
The theorem is very similar to Ceva's theorem
Ceva's theorem
Ceva's theorem is a theorem about triangles in plane geometry. Given a triangle ABC, let the lines AO, BO and CO be drawn from the vertices to a common point O to meet opposite sides at D, E and F respectively...
in that their equations differ only in sign.
Proof
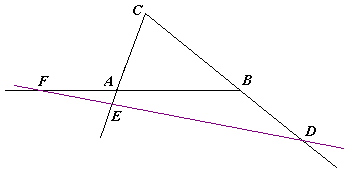
First, the sign of the left-hand side negative since either all three of the ratios are negative, the case where the line DEF misses the triangle (lower diagram), or one is negative and the other two are positive, the case where DEF crosses two sides of the triangle. (See Pasch's axiom
Pasch's axiom
In geometry, Pasch's axiom is a result of plane geometry used by Euclid, but yet which cannot be derived from Euclid's postulates. Its axiomatic role was discovered by Moritz Pasch.The axiom states that, in the plane,...
.)
To check the magnitude, construct perpendiculars from A, B, and C to the line DEF and let the lengths be a, b, and c respectively. Then by similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
triangles it follows that |AF/FB| = |a/b|, |BD/DC| = |b/c|, and |CE/EA| = c/a. So
For a simpler, if less symmetrical way to check the magnitude, draw CK parallel to AB where DEF meets CK at K. Then by similar triangles
and the result follows by eliminating CK from these equations.
The converse follows as a corollary. Let D, E and F be given on the lines BC, AC and AB so that the equation holds. Let F′ be the point where DE crosses AB. Then by the theorem, the equation also holds for D, E and F′. Comparing the two,
But at most one point can cut a segment in a given ratio so F=F′.
A non-computational proof using homothecies
The following proof uses only notions of affine geometryAffine geometry
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
, notably homothecies.
Whether or not D, E, F are collinear, there are three homothecies with centers D, E, F that respectively send B to C, C to A, and A to B. The composition of the three then is an element of the group of homothecy-translations that fixes B, so it is a homothecy with center B, possibly with ratio 1 (in which case it is the identity). This composition fixes the line DE if and only if F is collinear with D and E (since the first two homothecies certainly fix DE, and the third does so only if F lies on DE). Therefore D, E, F are collinear if and only if this composition is the identity, which means that the product of the three ratios is 1:
-

which is equivalent to the given equation.
History
It is uncertain who actually discovered the theorem, however the oldest extant exposition appears in Spherics by Menelaus. In this book, the plane version of the theorem is used as a lemma to prove a spherical version of the theorem.
In AlmagestAlmagestThe Almagest is a 2nd-century mathematical and astronomical treatise on the apparent motions of the stars and planetary paths. Written in Greek by Claudius Ptolemy, a Roman era scholar of Egypt,...
, PtolemyPtolemyClaudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
applies the theorem on a number of problems in spherical astronomy. During the Islamic Golden AgeIslamic Golden AgeDuring the Islamic Golden Age philosophers, scientists and engineers of the Islamic world contributed enormously to technology and culture, both by preserving earlier traditions and by adding their own inventions and innovations...
, Muslim scholars devoted a number of works that engaged in the study of Menelaus' theorem, which they referred to as "the proposition on the secants" (shakl al-qatta). The complete quadrilateral was called the "figure of secants" in their terminology. Al-BiruniAl-BiruniAbū al-Rayḥān Muḥammad ibn Aḥmad al-BīrūnīArabic spelling. . The intermediate form Abū Rayḥān al-Bīrūnī is often used in academic literature...
's work, The Keys of Astronomy, lists a number of those works, which can be classified into studies as part of commentaries on Ptolemy's Almagest as in the works of al-NayriziAl-NayriziAbū’l-‘Abbās al-Faḍl ibn Ḥātim al-Nairīzī was a 9th-10th century Persian mathematician and astronomer from Nayriz, Fars, Iran.He flourished under al-Mu'tadid, Caliph from 892 to 902, and compiled astronomical tables, writing a book for al-Mu'tadid on atmospheric phenomena.Nayrizi wrote...
and al-Khazin where each demonstrated particular cases of Menelaus' theorem that led to the sine rule, or works composed as independent treatises such as:
- The "Treatise on the Figure of Secants" (Risala fi shakl al-qatta) by Thabit ibn QurraThabit ibn Qurra' was a mathematician, physician, astronomer and translator of the Islamic Golden Age.Ibn Qurra made important discoveries in algebra, geometry and astronomy...
. - Husam al-DIn al-Salar's Removing the Veil from the Mysteries of the Figure of Secants (Kashf al-qina' 'an asrar al-shakl al-qatta'), also known as "The Book on the Figure of Secants" (Kitab al-shakl al-qatta) or in Europe as The Treatise on the Complete Quadrilateral. The lost treatise was referred to by Al-Tusi and Nasir al-Din al-TusiNasir al-Din al-TusiKhawaja Muḥammad ibn Muḥammad ibn Ḥasan Ṭūsī , better known as Naṣīr al-Dīn al-Ṭūsī , was a Persian polymath and prolific writer: an astronomer, biologist, chemist, mathematician, philosopher, physician, physicist, scientist, theologian and Marja Taqleed...
. - Work by al-SijziAl-SijziAbu Sa'id Ahmed ibn Mohammed ibn Abd Jalil Sijzi was a Persian astronomer and mathematician from Sistan, a region lying in the south-west of Afghanistan and south-east of Iran....
. - Tahdhib by Abu Nasr ibn Iraq.
External links
- Alternate proof of Menelaus' theorem, from PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
- Menelaus From Ceva
- Ceva and Menelaus Meet on the Roads
- Menelaus and Ceva at MathPages
- Menelaus' Theorem by Jay Warendorff. The Wolfram Demonstrations Project.
- The "Treatise on the Figure of Secants" (Risala fi shakl al-qatta) by Thabit ibn Qurra