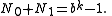Midy's theorem
Encyclopedia
In mathematics
, Midy's theorem, named after French
mathematician
E. Midy, is a statement about the decimal
expansion of fraction
s a/p where p is a prime
and a/p has a repeating decimal
expansion with an even period. If the period of the decimal representation of a/p is 2n, so that
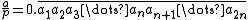
then the digits in the second half of the repeating decimal period are the 9s complement of the corresponding digits in its first half. In other words

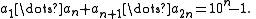
For example
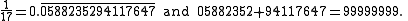
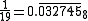
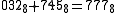
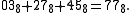
. However, it is also possible to prove Midy's theorem using elementary algebra
and modular arithmetic
:
Let p be a prime and a/p be a fraction between 0 and 1. Suppose the expansion of a/p in base b has a period of ℓ, so
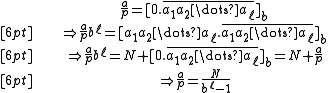
where N is the integer whose expansion in base b is the string a1a2...aℓ.
Note that b ℓ − 1 is a multiple of p because (b ℓ − 1)a/p is an integer. Also bn−1 is not a multiple of p for any value of n less than ℓ, because otherwise the repeating period of a/p in base b would be less than ℓ.
Now suppose that ℓ = hk. Then b ℓ − 1 is a multiple of bk − 1. Say b ℓ − 1 = m(bk − 1), so

But b ℓ − 1 is a multiple of p; bk − 1 is not a multiple of p (because k is less than ℓ ); and p is a prime; so m must be a multiple of p and
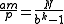
is an integer. In other words
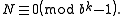
Now split the string a1a2...aℓ into h equal parts of length k, and let these represent the integers N0...Nh − 1 in base b, so that
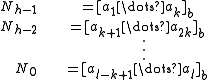
To prove Midy's extended theorem in base b we must show that the sum of the h integers Ni is a multiple of bk − 1.
Since bk is congruent to 1 modulo bk − 1, any power of bk will also be congruent to 1 modulo bk − 1. So
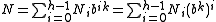
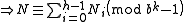

which proves Midy's extended theorem in base b.
To prove the original Midy's theorem, take the special case where h = 2. Note that N0 and N1 are both represented by strings of k digits in base b so both satisfy
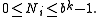
N0 and N1 cannot both equal 0 (otherwise a/p = 0) and cannot both equal bk − 1 (otherwise a/p = 1), so

and since N0 + N1 is a multiple of bk − 1, it follows that
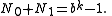
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Midy's theorem, named after French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
E. Midy, is a statement about the decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
expansion of fraction
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
s a/p where p is a prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
and a/p has a repeating decimal
Repeating decimal
In arithmetic, a decimal representation of a real number is called a repeating decimal if at some point it becomes periodic, that is, if there is some finite sequence of digits that is repeated indefinitely...
expansion with an even period. If the period of the decimal representation of a/p is 2n, so that
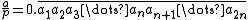
then the digits in the second half of the repeating decimal period are the 9s complement of the corresponding digits in its first half. In other words

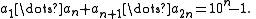
For example
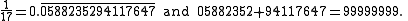
Midy's theorem in other bases
Midy's theorem and its extension do not depend on special properties of the decimal expansion, but work equally well in any base b, provided we replace 10k − 1 with bk − 1 and carry out addition in base b. For example, in octalOctal
The octal numeral system, or oct for short, is the base-8 number system, and uses the digits 0 to 7. Numerals can be made from binary numerals by grouping consecutive binary digits into groups of three...
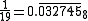
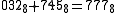
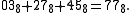
Proof of Midy's theorem
Short proofs of Midy's theorem can be given using results from group theoryGroup theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
. However, it is also possible to prove Midy's theorem using elementary algebra
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
and modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
:
Let p be a prime and a/p be a fraction between 0 and 1. Suppose the expansion of a/p in base b has a period of ℓ, so
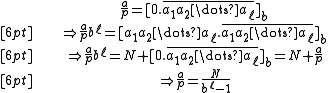
where N is the integer whose expansion in base b is the string a1a2...aℓ.
Note that b ℓ − 1 is a multiple of p because (b ℓ − 1)a/p is an integer. Also bn−1 is not a multiple of p for any value of n less than ℓ, because otherwise the repeating period of a/p in base b would be less than ℓ.
Now suppose that ℓ = hk. Then b ℓ − 1 is a multiple of bk − 1. Say b ℓ − 1 = m(bk − 1), so

But b ℓ − 1 is a multiple of p; bk − 1 is not a multiple of p (because k is less than ℓ ); and p is a prime; so m must be a multiple of p and
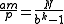
is an integer. In other words
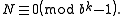
Now split the string a1a2...aℓ into h equal parts of length k, and let these represent the integers N0...Nh − 1 in base b, so that
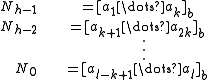
To prove Midy's extended theorem in base b we must show that the sum of the h integers Ni is a multiple of bk − 1.
Since bk is congruent to 1 modulo bk − 1, any power of bk will also be congruent to 1 modulo bk − 1. So
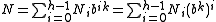
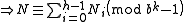

which proves Midy's extended theorem in base b.
To prove the original Midy's theorem, take the special case where h = 2. Note that N0 and N1 are both represented by strings of k digits in base b so both satisfy
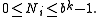
N0 and N1 cannot both equal 0 (otherwise a/p = 0) and cannot both equal bk − 1 (otherwise a/p = 1), so

and since N0 + N1 is a multiple of bk − 1, it follows that