Milü
Encyclopedia
The name Milü also known as Zulü (Zu
's ratio), is given to an approximation to π
(Pi
) found by Chinese mathematician and astronomer
Zu Chongzhi
. He computed π to be between 3.1415926 and 3.1415927 and gave two rational approximations of π,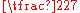
and 
, naming them respectively Yuelü 约率 (literally "approximate ratio") and Milü.
is by far the best rational
approximation of π
with a denominator of four digits or fewer, being accurate to 6 decimal places. It is within 0.000009% of the value of π, or in terms of common fractions overestimates π by less than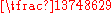
. The next rational number (ordered by size of denominator) that is a better rational approximation of π is 
, still only correct to 6 decimal places. To be accurate to 7 decimal places, one needs to go as far as 
.
Zu Chongzhi
Zu Chongzhi , courtesy name Wenyuan , was a prominent Chinese mathematician and astronomer during the Liu Song and Southern Qi Dynasties.-Life and works:...
's ratio), is given to an approximation to π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
(Pi
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
) found by Chinese mathematician and astronomer
Chinese astronomy
Astronomy in China has a very long history, with historians considering that "they [the Chinese] were the most persistent and accurate observers of celestial phenomena anywhere in the world before the Arabs."...
Zu Chongzhi
Zu Chongzhi
Zu Chongzhi , courtesy name Wenyuan , was a prominent Chinese mathematician and astronomer during the Liu Song and Southern Qi Dynasties.-Life and works:...
. He computed π to be between 3.1415926 and 3.1415927 and gave two rational approximations of π,
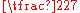and , naming them respectively Yuelü 约率 (literally "approximate ratio") and Milü. is by far the best rationalRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
approximation of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
with a denominator of four digits or fewer, being accurate to 6 decimal places. It is within 0.000009% of the value of π, or in terms of common fractions overestimates π by less than
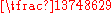. The next rational number (ordered by size of denominator) that is a better rational approximation of π is , still only correct to 6 decimal places. To be accurate to 7 decimal places, one needs to go as far as .-
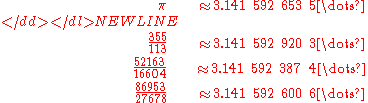
An easy mnemonicMnemonicA mnemonic , or mnemonic device, is any learning technique that aids memory. To improve long term memory, mnemonic systems are used to make memorization easier. Commonly encountered mnemonics are often verbal, such as a very short poem or a special word used to help a person remember something,...
helps memorize this useful fraction by writing down each of the first three odd numbers twice: 1 1 3 3 5 5, then dividing the decimal number represented by the last 3 digits by the decimal number given by the first three digits.
Zu's contemporary calendarist and mathematician He Chengtian invented a fraction interpolation method called "harmonization of the divisor of the day" to obtain a closer approximation by iteratively adding the numerators and denominators of a "weak" fraction and a "strong" fraction. Zu ChongzhiZu ChongzhiZu Chongzhi , courtesy name Wenyuan , was a prominent Chinese mathematician and astronomer during the Liu Song and Southern Qi Dynasties.-Life and works:...
's approximation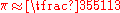
can be obtained with He's method
See also
- Continued fraction expansions of π
- History of numerical approximations of πNumerical approximations of πThis page is about the history of approximations for the mathematical constant pi . There is a table summarizing the chronology of computation of π. See also the history of pi for other aspects of the evolution of our knowledge about mathematical properties of pi...
- Pi Approximation Day