Miquel's theorem
Encyclopedia
Miquel's theorem is a theorem
in geometry
, named after Auguste Miquel, about the intersection
pattern of circles defined from six points on a triangle. From any triangle, and any three points on the three sides of the triangle, one may define three circles that each pass through a vertex of the triangle and the two points on its adjacent sides; Miquel's theorem states that these three circles meet in a single point, called the Miquel point.
Formally, let ABC be a triangle, and let A´, B´ and C´ be three points on sides BC, AC, and AB of the triangle, respectively. Draw three circles circumscribing the three triangles AB´C´, A´BC´, and A´B´C. Then Miquel's theorem states that these three circles intersect in a single point M, the Miquel point. In addition, the three angles MA´B, MB´C and MC´A (green in the diagram) are all equal to each other, as are the three angles MA´C, MB´A and MC´B.
If the fractional distances of points A´, B´ and C´ along the sides BC, CA and AB are respectively da, db and dc, and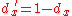
, the Miquel point is given in trilinear co-ordinates (x : y : z) by:
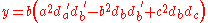
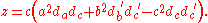
In the case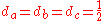
, the Miquel point is the circumcentre.
This theorem can be reversed to say that for any three circles intersecting at M, a line can be drawn from any point A on one of the circles, through C´ to the intersection, B, with another circle. This point is then connected to a point C of the third circle with a line passing through A´. Given this construction, C, B´ and A are collinear. That is to say, the triangle ABC will always pass though the points A´, B´ and C´.
This can be extended to a circle with four points. Given four points, A, B, C, and D on a circle, and four circles passing through each adjacent pair of points, the four intersections of adjacent circles (i.e., the circle pairs also sharing an intersection on the original circle) W, X, Y and Z also lie on a common circle. This result is known as Miquel's six circles theorem.
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, named after Auguste Miquel, about the intersection
Intersection
Intersection has various meanings in different contexts:*In mathematics and geometry**Intersection , the set of elements common to some collection of sets.**Line-line intersection**Line-plane intersection**Line–sphere intersection...
pattern of circles defined from six points on a triangle. From any triangle, and any three points on the three sides of the triangle, one may define three circles that each pass through a vertex of the triangle and the two points on its adjacent sides; Miquel's theorem states that these three circles meet in a single point, called the Miquel point.
Formally, let ABC be a triangle, and let A´, B´ and C´ be three points on sides BC, AC, and AB of the triangle, respectively. Draw three circles circumscribing the three triangles AB´C´, A´BC´, and A´B´C. Then Miquel's theorem states that these three circles intersect in a single point M, the Miquel point. In addition, the three angles MA´B, MB´C and MC´A (green in the diagram) are all equal to each other, as are the three angles MA´C, MB´A and MC´B.
If the fractional distances of points A´, B´ and C´ along the sides BC, CA and AB are respectively da, db and dc, and
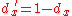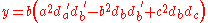
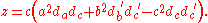
, the Miquel point is given in trilinear co-ordinates (x : y : z) by:In the case
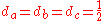, the Miquel point is the circumcentre.This theorem can be reversed to say that for any three circles intersecting at M, a line can be drawn from any point A on one of the circles, through C´ to the intersection, B, with another circle. This point is then connected to a point C of the third circle with a line passing through A´. Given this construction, C, B´ and A are collinear. That is to say, the triangle ABC will always pass though the points A´, B´ and C´.
This can be extended to a circle with four points. Given four points, A, B, C, and D on a circle, and four circles passing through each adjacent pair of points, the four intersections of adjacent circles (i.e., the circle pairs also sharing an intersection on the original circle) W, X, Y and Z also lie on a common circle. This result is known as Miquel's six circles theorem.