
Montgomery's pair correlation conjecture
Encyclopedia
In mathematics, Montgomery's pair correlation conjecture is a conjecture made by that the pair correlation between pairs of zeros of the Riemann zeta function (normalized to have unit average spacing) is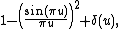
which, as Freeman Dyson
pointed out to him, is the same as the pair correlation function
of random Hermitian matrices. Informally, this means that the chance of finding a zero in a very short interval of length 2πL/log(T) at a distance 2πu/log(T) from a zero 1/2+iT is about L times the expression above. (The factor 2π/log(T) is a normalization factor that can be thought of informally as the average spacing between zeros with imaginary part about T.) showed that the conjecture was supported by large-scale computer calculations of the zeros. The conjecture has been extended to correlations of more than 2 zeros, and also to zeta functions of automorphic representations .
Montgomery was studying the Fourier transform F(x) of the pair correlation function, and showed (assuming the Riemann hypothesis) that it was
equal to |x| for |x|<1. His methods were unable to determine it for |x|≥1, but he conjectured that it was equal to 1 for these x, which implies that the pair correlation function is as above.
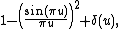
which, as Freeman Dyson
Freeman Dyson
Freeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
pointed out to him, is the same as the pair correlation function
Correlation function
A correlation function is the correlation between random variables at two different points in space or time, usually as a function of the spatial or temporal distance between the points...
of random Hermitian matrices. Informally, this means that the chance of finding a zero in a very short interval of length 2πL/log(T) at a distance 2πu/log(T) from a zero 1/2+iT is about L times the expression above. (The factor 2π/log(T) is a normalization factor that can be thought of informally as the average spacing between zeros with imaginary part about T.) showed that the conjecture was supported by large-scale computer calculations of the zeros. The conjecture has been extended to correlations of more than 2 zeros, and also to zeta functions of automorphic representations .
Montgomery was studying the Fourier transform F(x) of the pair correlation function, and showed (assuming the Riemann hypothesis) that it was
equal to |x| for |x|<1. His methods were unable to determine it for |x|≥1, but he conjectured that it was equal to 1 for these x, which implies that the pair correlation function is as above.

