Moran's I
Encyclopedia
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Moran's I is a measure of spatial autocorrelation developed by Patrick A.P. Moran
Patrick Alfred Pierce Moran
Patrick Alfred Pierce Moran FRS , commonly known as Pat Moran was an Australian statistician who made significant contributions to probability theory and its application to population and evolutionary genetics....
. Spatial autocorrelation is characterized by a correlation in a signal among nearby locations in space. Spatial autocorrelation is more complex than one-dimensional autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
because spatial correlation is multi-dimensional (i.e. 2 or 3 dimensions of space) and multi-directional.
Moran's I is defined as
where
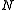is the number of spatial units indexed by 
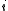and 
; 
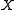is the variable of interest; 
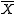is the mean of 
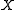; and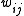 
is an element of a matrix of spatial weights.The expected value of Moran's I under hypothesis of no spatial autocorrelation is
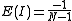
Its variance equals
where
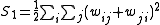
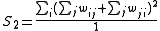
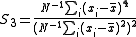
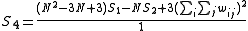
Negative (positive) values indicate negative (positive) spatial autocorrelation. Values range from −1 (indicating perfect dispersion) to +1 (perfect correlation). A zero value indicates a random spatial pattern. For statistical hypothesis testing, Moran's I values can be transformed to Z-scores in which values greater than 1.96 or smaller than −1.96 indicate spatial autocorrelation that is significant at the 5% level.
Moran's I is inversely related to Geary's C
Geary's C
Geary's C is a measure of spatial autocorrelation. Like autocorrelation, spatial autocorrelation means that adjacent observations of the same phenomenon are correlated. However, autocorrelation is about proximity in time. Spatial autocorrelation is about proximity in space...
, but it is not identical. Moran's I is a measure of global spatial autocorrelation, while Geary's C
Geary's C
Geary's C is a measure of spatial autocorrelation. Like autocorrelation, spatial autocorrelation means that adjacent observations of the same phenomenon are correlated. However, autocorrelation is about proximity in time. Spatial autocorrelation is about proximity in space...
is more sensitive to local spatial autocorrelation.