
Moreau's theorem
Encyclopedia
In mathematics
, Moreau's theorem is a result in convex analysis
. It shows that sufficiently well-behaved
convex function
als on Hilbert space
s are differentiable and the derivative is well-approximated by the so-called Yosida approximation, which is defined in terms of the resolvent operator.
extended real-valued functional
on H. Let A stand for ∂φ, the subderivative
of φ; for α > 0 let Jα denote the resolvent:
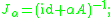
and let Aα denote the Yosida approximation to A:
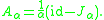
For each α > 0 and x ∈ H, let
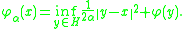
Then
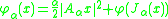
and φα is convex and Fréchet differentiable
with derivative dφα = Aα. Also, for each x ∈ H (pointwise), φα(x) converges upwards to φ(x) as α → 0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Moreau's theorem is a result in convex analysis
Convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
. It shows that sufficiently well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
als on Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s are differentiable and the derivative is well-approximated by the so-called Yosida approximation, which is defined in terms of the resolvent operator.
Statement of the theorem
Let H be a Hilbert space and let φ : H → R ∪ {+∞} be a proper, convex and lower semi-continuousSemi-continuity
In mathematical analysis, semi-continuity is a property of extended real-valued functions that is weaker than continuity...
extended real-valued functional
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
on H. Let A stand for ∂φ, the subderivative
Subderivative
In mathematics, the concepts of subderivative, subgradient, and subdifferential arise in convex analysis, that is, in the study of convex functions, often in connection to convex optimization....
of φ; for α > 0 let Jα denote the resolvent:
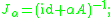
and let Aα denote the Yosida approximation to A:
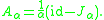
For each α > 0 and x ∈ H, let
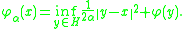
Then
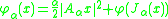
and φα is convex and Fréchet differentiable
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
with derivative dφα = Aα. Also, for each x ∈ H (pointwise), φα(x) converges upwards to φ(x) as α → 0.

