
Muirhead's inequality
Encyclopedia
In mathematics
, Muirhead's inequality, named after Robert Franklin Muirhead
, also known as the "bunching" method, generalizes the inequality of arithmetic and geometric means
.
vector

define the "a-mean" [a] of nonnegative real numbers x1, ..., xn by

where the sum extends over all permutation
s σ of { 1, ..., n }.
In case a = (1, 0, ..., 0), this is just the ordinary arithmetic mean
of x1, ..., xn. In case a = (1/n, ..., 1/n), it is the geometric mean
of x1, ..., xn. (When n = 2, this is the Heinz mean.)
precisely if both P and its transpose PT are stochastic matrices
. A stochastic matrix is a square matrix of nonnegative real entries in which the sum of the entries in each column is 1. Thus, a doubly stochastic matrix is a square matrix of nonnegative real entries in which the sum of the entries in each row and the sum of the entries in each column is 1.
The proof makes use of the fact that every doubly stochastic matrix is a weighted average of permutation matrices
(Birkhoff-von Neumann theorem).


Then the existence of a doubly stochastic matrix P such that a = Pb is equivalent to the following system of inequalities:




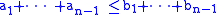

(The last one is an equality; the others are weak inequalities.)
The sequence is said to majorize the sequence
is said to majorize the sequence  .
.
 ) majorizes the other one.
) majorizes the other one.

This notation requires developing every permutation, developing an expression made of n! monomials, for instance:



we have




then
which is

yielding the inequality.
We transform it in the symmetric-sum notation:

The sequence (2, 0) majorizes the sequence (1, 1), thus the inequality holds by bunching. Again,


which yields
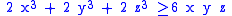
the sequence (3, 0, 0) majorizes the sequence (1, 1, 1), thus the inequality holds by bunching.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Muirhead's inequality, named after Robert Franklin Muirhead
Robert Franklin Muirhead
Robert Franklin Muirhead , was a Scottish mathematician who discovered Muirhead's inequality.-Early life and education:Born at Shawlands, Glasgow, in January 1860, Robert Franklyn Muirhead received his early education from private tutors and the village school at Lochwinnoch...
, also known as the "bunching" method, generalizes the inequality of arithmetic and geometric means
Inequality of arithmetic and geometric means
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if...
.
The "a-mean"
For any realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

define the "a-mean" [a] of nonnegative real numbers x1, ..., xn by

where the sum extends over all permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s σ of { 1, ..., n }.
In case a = (1, 0, ..., 0), this is just the ordinary arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
of x1, ..., xn. In case a = (1/n, ..., 1/n), it is the geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
of x1, ..., xn. (When n = 2, this is the Heinz mean.)
Doubly stochastic matrices
An n × n matrix P is doubly stochasticDoubly stochastic matrix
In mathematics, especially in probability and combinatorics, a doubly stochastic matrix,is a square matrix of nonnegative real numbers, each of whose rows and columns sums to 1...
precisely if both P and its transpose PT are stochastic matrices
Stochastic matrix
In mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
. A stochastic matrix is a square matrix of nonnegative real entries in which the sum of the entries in each column is 1. Thus, a doubly stochastic matrix is a square matrix of nonnegative real entries in which the sum of the entries in each row and the sum of the entries in each column is 1.
The inequality
Muirhead's inequality states that [a] ≤ [b] for all xi ≥ 0 if and only if there is some doubly stochastic matrix P for which a = Pb.The proof makes use of the fact that every doubly stochastic matrix is a weighted average of permutation matrices
Permutation matrix
In mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
(Birkhoff-von Neumann theorem).
Another equivalent condition
Because of the symmetry of the sum, no generality is lost by sorting the exponents into decreasing order:

Then the existence of a doubly stochastic matrix P such that a = Pb is equivalent to the following system of inequalities:




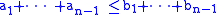

(The last one is an equality; the others are weak inequalities.)
The sequence
 is said to majorize the sequence
is said to majorize the sequence  .
.Symmetric sum-notation tricks
It is useful to use a kind of special notation for the sums. A success in reducing an inequality in this form means that the only condition for testing it is to verify whether one exponent sequence ( ) majorizes the other one.
) majorizes the other one.
This notation requires developing every permutation, developing an expression made of n! monomials, for instance:

Deriving the arithmetic-geometric mean inequality
Let

we have




then
- [aA] ≥ [aG]
which is

yielding the inequality.
Examples
Suppose you want to prove that x2 + y2 ≥ 2xy by using bunching (Muirhead's inequality):We transform it in the symmetric-sum notation:

The sequence (2, 0) majorizes the sequence (1, 1), thus the inequality holds by bunching. Again,


which yields
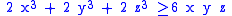
the sequence (3, 0, 0) majorizes the sequence (1, 1, 1), thus the inequality holds by bunching.

