In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, Novikov's compact leaf theorem, named after Sergei Novikov, states that

A codimension-one foliation

Foliation

In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....

 of a compact 3-manifold whose universal covering space is not contractible must have a compact leaf.

Novikov's compact leaf theorem for S³

Theorem: A smooth codimension-one foliation of the 3-sphere

3-sphere

In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...

S³ has a compact leaf. The leaf is a torus T² bounding a solid torus

Solid torus

In mathematics, a solid torus is a topological space homeomorphic to S^1 \times D^2, i.e. the cartesian product of the circle with a two dimensional disc endowed with the product topology. The solid torus is a connected, compact, orientable 3-dimensional manifold with boundary...

 with the Reeb foliation

Reeb foliation

In mathematics, the Reeb foliation is a particular foliation of the 3-sphere, introduced by the French mathematician Georges Reeb .It is based on dividing the sphere into two solid tori, along a 2-torus: see Clifford torus. Each of the solid tori is then foliated internally, in codimension 1, and...

.

The theorem was proved by Sergey Novikov in 1964. Earlier Charles Ehresmann

Charles Ehresmann

Charles Ehresmann was a French mathematician who worked on differential topology and category theory. He is known for work on the topology of Lie groups, the jet concept , and his seminar on category theory.He attended the École Normale Supérieure in Paris before performing one year of military...

 had conjectured that every smooth codimension-one foliation on S³ had a compact leaf, which was true for all known examples; in particular, Reeb foliation

Reeb foliation

In mathematics, the Reeb foliation is a particular foliation of the 3-sphere, introduced by the French mathematician Georges Reeb .It is based on dividing the sphere into two solid tori, along a 2-torus: see Clifford torus. Each of the solid tori is then foliated internally, in codimension 1, and...

 had a compact leaf that was T².

Novikov's compact leaf theorem for any M³

In 1965, Novikov proved the compact leaf theorem for any M³:

Theorem: Let M³ be a closed 3-manifold with a smooth codimension-one foliation F. Suppose any of the following conditions is satisfied:

1. the fundamental group
   Fundamental group
   In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
   
     is finite,
2. the second homotopy group
   Homotopy group
   In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
   
    ,
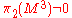3. there exists a leaf 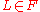such that the map 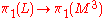induced by inclusion has a non-trivial kernel
   Kernel (mathematics)
   In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
   
   .

Then F has a compact leaf of genus

Genus

In biology, a genus is a low-level taxonomic rank used in the biological classification of living and fossil organisms, which is an example of definition by genus and differentia...

g ≤ 1.
In terms of covering spaces:

A codimension-one foliation

Foliation

In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....

 of a compact 3-manifold whose universal covering space is not contractible must have a compact leaf.