
Néron–Tate height
Encyclopedia
In number theory
, the Néron–Tate height (or canonical height) is a quadratic form on the Mordell-Weil group of rational points of an abelian variety
defined over a global field
. It is named after André Néron
and John Tate
.
Tate (unpublished) defined it globally by observing that the logarithmic height hL associated to an invertible sheaf
L on an abelian variety
A is “almost quadratic,” and used this to show that the limit
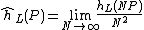
exists and defines a quadratic form on the Mordell-Weil group of rational points.
The Néron–Tate height depends on the choice of an invertible sheaf (or an element of the Néron-Severi group) on the abelian variety. If the abelian variety A is defined over a number field K and the invertible sheaf is ample, then the Néron–Tate height is positive definite in the sense that it vanishes only on torsion elements of the Mordell-Weil group A(K). More generally, induces a positive definite quadratic form on the real vector space
induces a positive definite quadratic form on the real vector space 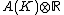 .
.
On an elliptic curve
, the Néron-Severi group is of rank one and has a unique ample generator, so this generator is often used to define the Néron–Tate height, which is denoted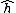 without reference to a particular line bundle. (However, the height that naturally appears in the statement of the Birch–Swinnerton-Dyer conjecture is twice this height.) On abelian varieties of higher dimension, there need not be a particular choice of smallest ample line bundle to be used in defining the Néron–Tate height.
without reference to a particular line bundle. (However, the height that naturally appears in the statement of the Birch–Swinnerton-Dyer conjecture is twice this height.) On abelian varieties of higher dimension, there need not be a particular choice of smallest ample line bundle to be used in defining the Néron–Tate height.
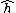 on an elliptic curve E is
on an elliptic curve E is
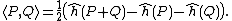
The elliptic regulator of E/K is
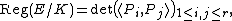
where P1,…,Pr is a basis for the Mordell-Weil group E(K) modulo torsion (cf. Gram determinant). The elliptic regulator does not depend on the choice of basis.
More generally, let A/K be an abelian variety, let B ≅ Pic0(A) be the dual abelian variety to A, and let P be the Poincaré line bundle on A × B. Then the abelian regulator of A/K is defined by choosing a basis Q1,…,Qr for the Mordell-Weil group A(K) modulo torsion and a basis η1,…,ηr for the Mordell-Weil group B(K) modulo torsion and setting
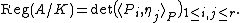
(The definitions of elliptic and abelian regulator are not entirely consistent, since if A is an elliptic curve, then the latter is 2r times the former.)
The elliptic and abelian regulators appear in the Birch–Swinnerton-Dyer conjecture.
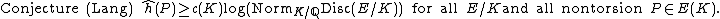

In both conjectures, the constants are positive and depend only on the indicated quantities. It is known that the abc conjecture
implies Lang's conjecture. The best general result on Lehmer's conjecture is the weaker estimate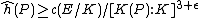 due to Masser
due to Masser
. When the elliptic curve has complex multiplication
, this has been improved to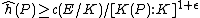 by Laurent.
by Laurent.
is a triple (V,φ,L) consisting of a (smooth projective) algebraic variety V, a self-morphism φ : V → V, and a line bundle L on V with the property that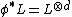 for some integer d > 1. The associated canonical height is given by the Tate limit
for some integer d > 1. The associated canonical height is given by the Tate limit
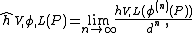
where φ(n) = φ o φ o … o φ is the n-fold iteration of φ. For example, any morphism φ : PN → PN of degree d > 1 yields a canonical height associated to the line bundle relation φ*O(1) = O(d). If V is defined over a number field and L is ample, then the canonical height is non-negative, and

(P is preperiodic if its forward orbit P, φ(P), φ2(P), φ3(P),… contains only finitely many distinct points.)
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Néron–Tate height (or canonical height) is a quadratic form on the Mordell-Weil group of rational points of an abelian variety
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
defined over a global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
. It is named after André Néron
André Néron
André Néron was a French mathematician at the Université de Poitiers who worked on elliptic curves and Abelian varieties...
and John Tate
John Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
.
Definition and properties
Néron defined the Néron–Tate height as a sum of local heights.Tate (unpublished) defined it globally by observing that the logarithmic height hL associated to an invertible sheaf
Invertible sheaf
In mathematics, an invertible sheaf is a coherent sheaf S on a ringed space X, for which there is an inverse T with respect to tensor product of OX-modules. It is the equivalent in algebraic geometry of the topological notion of a line bundle...
L on an abelian variety
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
A is “almost quadratic,” and used this to show that the limit
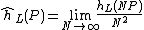
exists and defines a quadratic form on the Mordell-Weil group of rational points.
The Néron–Tate height depends on the choice of an invertible sheaf (or an element of the Néron-Severi group) on the abelian variety. If the abelian variety A is defined over a number field K and the invertible sheaf is ample, then the Néron–Tate height is positive definite in the sense that it vanishes only on torsion elements of the Mordell-Weil group A(K). More generally,
 induces a positive definite quadratic form on the real vector space
induces a positive definite quadratic form on the real vector space 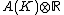 .
.On an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
, the Néron-Severi group is of rank one and has a unique ample generator, so this generator is often used to define the Néron–Tate height, which is denoted
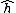 without reference to a particular line bundle. (However, the height that naturally appears in the statement of the Birch–Swinnerton-Dyer conjecture is twice this height.) On abelian varieties of higher dimension, there need not be a particular choice of smallest ample line bundle to be used in defining the Néron–Tate height.
without reference to a particular line bundle. (However, the height that naturally appears in the statement of the Birch–Swinnerton-Dyer conjecture is twice this height.) On abelian varieties of higher dimension, there need not be a particular choice of smallest ample line bundle to be used in defining the Néron–Tate height.The elliptic and abelian regulators
The bilinear form associated to the canonical height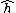 on an elliptic curve E is
on an elliptic curve E is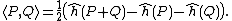
The elliptic regulator of E/K is
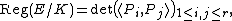
where P1,…,Pr is a basis for the Mordell-Weil group E(K) modulo torsion (cf. Gram determinant). The elliptic regulator does not depend on the choice of basis.
More generally, let A/K be an abelian variety, let B ≅ Pic0(A) be the dual abelian variety to A, and let P be the Poincaré line bundle on A × B. Then the abelian regulator of A/K is defined by choosing a basis Q1,…,Qr for the Mordell-Weil group A(K) modulo torsion and a basis η1,…,ηr for the Mordell-Weil group B(K) modulo torsion and setting
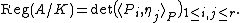
(The definitions of elliptic and abelian regulator are not entirely consistent, since if A is an elliptic curve, then the latter is 2r times the former.)
The elliptic and abelian regulators appear in the Birch–Swinnerton-Dyer conjecture.
Lower bounds for the Néron–Tate height
There are two fundamental conjectures that give lower bounds for the Néron–Tate height. In the first, the field K is fixed and the elliptic curve E/K and point P ∈ E(K) vary, while in the second, the curve E/K is fixed while the field of definition of the point P varies.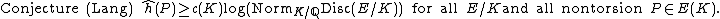

In both conjectures, the constants are positive and depend only on the indicated quantities. It is known that the abc conjecture
Abc conjecture
The abc conjecture is a conjecture in number theory, first proposed by Joseph Oesterlé and David Masser in 1985. The conjecture is stated in terms of three positive integers, a, b and c , which have no common factor and satisfy a + b = c...
implies Lang's conjecture. The best general result on Lehmer's conjecture is the weaker estimate
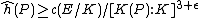 due to Masser
due to MasserDavid Masser
David William Masser is Professor of Mathematics at the University of Basel, in Basel, Switzerland. He obtained his Ph.D. from University of Cambridge in 1974 on the topic of Elliptic Functions and Transcendence....
. When the elliptic curve has complex multiplication
Complex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
, this has been improved to
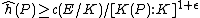 by Laurent.
by Laurent.Generalizations
A polarized algebraic dynamical systemArithmetic dynamics
Arithmetic dynamicsis a field that amalgamates two areas of mathematics, dynamical systems and number theory.Classically, discrete dynamics refers to the study of the iteration of self-maps of the complex plane or real line...
is a triple (V,φ,L) consisting of a (smooth projective) algebraic variety V, a self-morphism φ : V → V, and a line bundle L on V with the property that
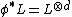 for some integer d > 1. The associated canonical height is given by the Tate limit
for some integer d > 1. The associated canonical height is given by the Tate limit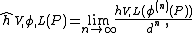
where φ(n) = φ o φ o … o φ is the n-fold iteration of φ. For example, any morphism φ : PN → PN of degree d > 1 yields a canonical height associated to the line bundle relation φ*O(1) = O(d). If V is defined over a number field and L is ample, then the canonical height is non-negative, and

(P is preperiodic if its forward orbit P, φ(P), φ2(P), φ3(P),… contains only finitely many distinct points.)

