
Pascal's calculator
Encyclopedia

Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
invented the mechanical calculator
Mechanical calculator
A mechanical calculator is a device used to perform the basic operations of arithmetic. Mechanical calculators are comparable in size to small desktop computers and have been rendered obsolete by the advent of the electronic calculator....
in 1642. He conceived it while trying to help his father who had been assigned the task of reorganizing the tax revenues of the French province of Haute-Normandie
Haute-Normandie
Upper Normandy is one of the 27 regions of France. It was created in 1984 from two départements: Seine-Maritime and Eure, when Normandy was divided into Lower Normandy and Upper Normandy. This division continues to provoke controversy, and some continue to call for reuniting the two regions...
; first called Arithmetic Machine, Pascal's Calculator and later Pascaline, it could add and subtract directly and multiply and divide by repetition.
Pascal went through 50 prototypes before presenting his first machine to the public in 1645. He dedicated it to Pierre Séguier
Pierre Séguier
-Early years:Born in Paris, France of a prominent legal family originating in Quercy. His grandfather, Pierre Séguier , was président à mortier in the parlement of Paris from 1554 to 1576, and the chancellor's father, Jean Séguier, a seigneur d'Autry, was civil lieutenant of Paris at the time of...
, the chancellor of France at the time. He built around twenty more machines during the next decade, often improving on his original design. Nine machines have survived the centuries, most of them being on display in European museums. In 1649 a royal privilege, signed by Louis XIV of France
Louis XIV of France
Louis XIV , known as Louis the Great or the Sun King , was a Bourbon monarch who ruled as King of France and Navarre. His reign, from 1643 to his death in 1715, began at the age of four and lasted seventy-two years, three months, and eighteen days...
, gave him the exclusivity of the design and manufacturing of calculating machines in France.
Its introduction launched the development of mechanical calculators in Europe first and then all over the world, development which culminated, three centuries later, in the invention of the microprocessor
Intel 4004
The Intel 4004 was a 4-bit central processing unit released by Intel Corporation in 1971. It was the first complete CPU on one chip, and also the first commercially available microprocessor...
developed for a Busicom
Busicom
Busicom was a Japanese company that owned the rights to the first microprocessor, the Intel 4004, which they created in partnership with Intel in 1970....
calculator in 1971.
The mechanical calculator industry owes a lot of its key machines and inventions to the pascaline. First Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
invented his Leibniz wheel
Leibniz wheel
A Leibniz wheel or stepped drum was a cylinder with a set of teeth of incremental length which, when coupled to a counting wheel, was used in the calculating engine of a class of mechanical calculators...
s after 1671 while trying to add an automatic multiplication and division feature to the pascaline, then Thomas de Colmar drew his inspiration from Pascal and Leibniz when he designed his arithmometer
Arithmometer
An Arithmometer or Arithmomètre was a mechanical calculator that could add and subtract directly and could perform long multiplications and divisions effectively by using a movable accumulator for the result. Patented in France by Thomas de Colmar in 1820 and manufactured from 1851 to 1915, it...
in 1820, and finally Dorr E. Felt substituted the input wheels of the pascaline by columns of keys to invent his comptometer
Comptometer
The comptometer was the first commercially successful key-driven mechanical calculator, patented in the USA by Dorr E. Felt in 1887.A key-driven calculator is extremely fast because each key adds or subtracts its value to the accumulator as soon as it is pressed and a skilled operator can enter all...
around 1887. The pascaline was also constantly improved upon, especially with the machines of Dr. Roth around 1840, and then with some portable machines until the creation of the first electronic calculators.
From antiquity to the renaissance
A short list of precursors to the mechanical calculator must include the Antikythera mechanismAntikythera mechanism
The Antikythera mechanism is an ancient mechanical computer designed to calculate astronomical positions. It was recovered in 1900–1901 from the Antikythera wreck. Its significance and complexity were not understood until decades later. Its time of construction is now estimated between 150 and 100...
from around 100 BC, early mechanical clocks and geared astrolabes ; they were all made of toothed gears linked by some sort of carry mechanisms.

Automaton
An automaton is a self-operating machine. The word is sometimes used to describe a robot, more specifically an autonomous robot. An alternative spelling, now obsolete, is automation.-Etymology:...
s were also precursors to the calculating machine.
An odometer
Odometer
An odometer or odograph is an instrument that indicates distance traveled by a vehicle, such as a bicycle or automobile. The device may be electronic, mechanical, or a combination of the two. The word derives from the Greek words hodós and métron...
, instrument for measuring distances, was first described around 25 BC by the roman engineer Vitruvius
Vitruvius
Marcus Vitruvius Pollio was a Roman writer, architect and engineer, active in the 1st century BC. He is best known as the author of the multi-volume work De Architectura ....
in the tenth volume of his De architectura
De architectura
' is a treatise on architecture written by the Roman architect Vitruvius and dedicated to his patron, the emperor Caesar Augustus, as a guide for building projects...
. It was made of a set of toothed gears linked by a carry mechanism ; the first one was driven by one of the chariot wheels and the last one dropped a small pebble in a bag for each Roman mile traveled.
A Chinese text of the third century AD described a chariot equipped with a geared mechanism that operated two wooden figures. One would strike a drum for every Chinese Li
Li (unit)
The li is a traditional Chinese unit of distance, which has varied considerably over time but now has a standardized length of 500 meters or half a kilometer...
traveled, the other one would strike a gong for every ten Li traveled.
Around the end of the tenth century, the French monk Gerbert d'Aurillac, whose abacus taught the Hindu-Arabic numeral system
Hindu-Arabic numeral system
The Hindu–Arabic numeral system or Hindu numeral system is a positional decimal numeral system developed between the 1st and 5th centuries by Indian mathematicians, adopted by Persian and Arab mathematicians , and spread to the western world...
to the Europeans, brought back from Spain the drawings of a machine invented by the Moors
Moors
The description Moors has referred to several historic and modern populations of the Maghreb region who are predominately of Berber and Arab descent. They came to conquer and rule the Iberian Peninsula for nearly 800 years. At that time they were Muslim, although earlier the people had followed...
that answered Yes or No to the questions it was asked (binary arithmetic) ; but its existence is contested.
Again in the thirteenth century, the monks Albertus Magnus
Albertus Magnus
Albertus Magnus, O.P. , also known as Albert the Great and Albert of Cologne, is a Catholic saint. He was a German Dominican friar and a bishop, who achieved fame for his comprehensive knowledge of and advocacy for the peaceful coexistence of science and religion. Those such as James A. Weisheipl...
and Roger Bacon
Roger Bacon
Roger Bacon, O.F.M. , also known as Doctor Mirabilis , was an English philosopher and Franciscan friar who placed considerable emphasis on the study of nature through empirical methods...
built talking heads made of earthware without any further development (Albertus Magnus complained that he had wasted forty years of his life when Thomas Aquinas
Thomas Aquinas
Thomas Aquinas, O.P. , also Thomas of Aquin or Aquino, was an Italian Dominican priest of the Catholic Church, and an immensely influential philosopher and theologian in the tradition of scholasticism, known as Doctor Angelicus, Doctor Communis, or Doctor Universalis...
, terrified by his machine, destroyed it).
The Italian polymath
Polymath
A polymath is a person whose expertise spans a significant number of different subject areas. In less formal terms, a polymath may simply be someone who is very knowledgeable...
Leonardo da Vinci
Leonardo da Vinci
Leonardo di ser Piero da Vinci was an Italian Renaissance polymath: painter, sculptor, architect, musician, scientist, mathematician, engineer, inventor, anatomist, geologist, cartographer, botanist and writer whose genius, perhaps more than that of any other figure, epitomized the Renaissance...
drew an odometer before 1519.
In 1525, the French craftsman Jean Fernel built the first pedometer
Pedometer
A pedometer is a device, usually portable and electronic or electromechanical, that counts each step a person takes by detecting the motion of the person's hips...
. It was made in the shape of a watch and had 4 dials (units, tens, hundreds, thousands) linked by a carry mechanism.
Pascal versus Schickard
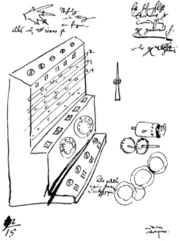
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
's work, announced that the drawings of a previously unknown calculating clock, predating Pascal's work by twenty years, had been found in two letters that Wilhelm Schickard
Wilhelm Schickard
Wilhelm Schickard was a German polymath who designed a calculating machine in 1623, twenty years before the Pascaline of Blaise Pascal. Unfortunately a fire destroyed the machine as it was being built in 1624 and Schickard decided to abandon his project...
had written to his friend Johannes Kepler in 1623 and 1624. This machine had stayed unknown for three centuries because it was destroyed in a fire as it was being built by Johann Pfister, a local craftsman, and Schickard abandoned his project.
Dr. von Freytag Loringhoff, a mathematics professor at the University of Tübingen built the first replica of Schickard's machine but he had to improve on the design of the carry mechanism:
Without this twentieth century improvement in the carry mechanism, which is not described in any of Schickard's letters or drawings, the replicas would not have worked. Another problem was found after the replicas were built:
.jpg)
Just as the Wright brothers
Wright brothers
The Wright brothers, Orville and Wilbur , were two Americans credited with inventing and building the world's first successful airplane and making the first controlled, powered and sustained heavier-than-air human flight, on December 17, 1903...
were credited for the first flight and therefore the invention of the airplane while Clément Ader
Clément Ader
Clément Ader was a French inventor and engineer born in Muret, Haute Garonne, and is remembered primarily for his pioneering work in aviation.- The inventor :...
flew 13 years before them, and Thomas Edison
Thomas Edison
Thomas Alva Edison was an American inventor and businessman. He developed many devices that greatly influenced life around the world, including the phonograph, the motion picture camera, and a long-lasting, practical electric light bulb. In addition, he created the world’s first industrial...
was credited with the invention of the incandescent light bulb while ten people had already worked on it before, Blaise Pascal is credited as the inventor of the mechanical calculator because he was the first person to present a machine that had all the parts required for its use, that had adequate solutions to all its challenges, a primitive machine, complete and ready to evolve.
Johannes Kepler, the recipient of Schickard's letters, died before Pascal's calculator was released to the public but he witnessed a similar duality of early precursor versus inventor with the invention of Logarithms:
Discovered in the second half of the twentieth century, Schickard's calculating clock had no influence on the development of mechanical calculators.
Achievements
Besides being the first calculating machine made public during its time, the pascaline is also:- the first calculator to be used in an office (his father's to compute taxes)
- the first calculator commercialized (with around twenty machines built)
- the first calculator to be patented (royal privilege of 1649)
- the first calculator to be described in an encyclopaedia (Diderot & d'Alembert, 1751):
- the first calculator sold by a distributor:
- the first calculator to be cloned (a clockmaker from Rouen before 1645)
- the first calculator to have a controlled carry mechanism which allowed for an effective propagation of multiple carries
Development
Pascal began to work on his calculator in 1642, when he was only 19 years old. He had been assisting his father, who worked as a tax commissioner, and sought to produce a device which could reduce some of his workload. Pascal received a Royal PrivilegePatent
A patent is a form of intellectual property. It consists of a set of exclusive rights granted by a sovereign state to an inventor or their assignee for a limited period of time in exchange for the public disclosure of an invention....
in 1649 that granted him exclusive rights to make and sell calculating machines in France. By 1654 Pascal had sold about twenty machines, but the cost and complexity of the Pascaline was a barrier to further sales, and production ceased in that year. By that time Pascal had moved on to the study of religion
Religion
Religion is a collection of cultural systems, belief systems, and worldviews that establishes symbols that relate humanity to spirituality and, sometimes, to moral values. Many religions have narratives, symbols, traditions and sacred histories that are intended to give meaning to life or to...
and philosophy
Philosophy
Philosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
which gave us both the Lettres provinciales
Lettres provinciales
The Lettres provinciales are a series of eighteen letters written by French philosopher and theologian Blaise Pascal under the pseudonym Louis de Montalte...
and the Pensées
Pensées
The Pensées represented a defense of the Christian religion by Blaise Pascal, the renowned 17th century philosopher and mathematician. Pascal's religious conversion led him into a life of asceticism, and the Pensées was in many ways his life's work. "Pascal's Wager" is found here...
.
Literary Praise
Pascal's genius and his machine have been celebrated all around the world for centuries.Fields of application
Pascalines came in both decimalDecimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
and non-decimal varieties, both of which exist in museums today. They were designed to be used by scientists, accountants and surveyors. The simplest Pascaline had five dials ; later production variants had up to ten dials.
The contemporary French currency
French livre
The livre was the currency of France until 1795. Several different livres existed, some concurrently. The livre was the name of both units of account and coins.-Etymology:...
system used livres, sols and deniers with 20 sols to a livre and 12 deniers to a sol.
Length was measured in toise
Toise
A toise is a unit of measure for length, area and volume originating in pre-revolutionary France. In North America, it was used in colonial French establishments in early New France, French Louisiana , and Quebec...
s, pieds, pouces and lignes
French units of measurement
France has a unique history of units of measurement due to radical attempts to adopt a metric system following the French Revolution.In the Ancien régime, before 1795, France used a system of measures that had many of the characteristics of the modern Imperial System of units...
with 6 pieds to a toise, 12 pouces to a pied and 12 lignes to a pouce. Therefore the pascaline needed wheels in base 6, 10, 12 and 20. Non decimal wheels were always located before the decimal part.
In an accounting machine (..10,10,20,12), the decimal part counted the number of livres (20 sols), sols (12 deniers) and deniers.
In a surveyor's machine (..10,10,6,12,12), the decimal part counted the number of toises (6 pieds), pieds (12 pouces), pouces (12 lignes) and lignes.
Scientific machines just had decimal wheels.
| Machine Type | All the other wheels | 4th wheel | 3rd wheel | 2nd wheel | 1st wheel |
|---|---|---|---|---|---|
| Decimal / Scientific |
base 10 Ten thousands... |
base 10 Thousands |
base 10 Hundreds |
base 10 Tens |
base 10 Units |
| Accounting | base 10 Hundreds... |
base 10 Tens |
base 10 Livres |
base 20 Sols |
base 12 Deniers |
| Surveying | base 10 Tens ... |
base 10 Toises |
base 6 Pieds |
base 12 Pouces |
base 12 Lignes |
| The decimal part of each machine is highlighted in yellow | |||||
The metric system was adopted in France on by which time Pascal's basic design had inspired other craftsmen, although with a similar lack of commercial success. Child prodigy Gottfried Wilhelm Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
devised a competing design, the Stepped Reckoner
Stepped Reckoner
The Step Reckoner was a digital mechanical calculator invented by German mathematician Gottfried Wilhelm Leibniz around 1672 and completed in 1694. The name comes from the translation of the German term for its operating mechanism; staffelwalze meaning 'stepped drum'...
, in 1671 which could perform addition, subtraction, multiplication and division; Leibniz struggled for forty years to perfect his design and produce sufficiently reliable machines.
Calculating machines did not become commercially viable until the early 19th century, when Charles Xavier Thomas de Colmar's
Charles Xavier Thomas
Charles Xavier Thomas de Colmar was a French inventor and entrepreneur best known for designing, patenting and manufacturing the first commercially successful mechanical calculator, the Arithmometer and for founding the insurance companies "Le Soleil" and "L'aigle" which, under his leadership,...
Arithmometer
Arithmometer
An Arithmometer or Arithmomètre was a mechanical calculator that could add and subtract directly and could perform long multiplications and divisions effectively by using a movable accumulator for the result. Patented in France by Thomas de Colmar in 1820 and manufactured from 1851 to 1915, it...
, itself using the key break through of Leibniz's design, was commercially successful.
Known machines
Most of the machines that have survived the centuries are of the accounting type. Seven of them are in European museums, one belongs to the IBM corporation and one is in private hands.| Location |
Country |
Machine Name |
Type |
Wheels |
Configuration |
Notes |
|---|---|---|---|---|---|---|
| CNAM museum Musée des Arts et Métiers The Musée des Arts et Métiers is a museum in Paris that houses the collection of the Conservatoire National des Arts et Métiers , which was founded in 1794 as a repository for the preservation of scientific instruments and inventions.-History:Since its foundation, the museum has been housed in the... Paris |
France | Chancelier Séguier | Accounting | 8 | 6 x 10 + 20 + 12 | |
| CNAM museum Paris |
France | Christina, Queen of Sweden | Scientific | 6 | 6 x 10 | |
| CNAM museum Paris |
France | Louis Périer | Accounting | 8 | 6 x 10 + 20 + 12 | Louis Périer, Pascal's nephew, offered it to the Académie des sciences de Paris in 1711. |
| CNAM museum Paris |
France | Late (Tardive) | Accounting | 6 | 4 x 10 + 20 + 12 | This machine was assembled in the XVIIIth century with unused parts. |
| musée Henri Lecoq Clermont-Ferrand Clermont-Ferrand Clermont-Ferrand is a city and commune of France, in the Auvergne region, with a population of 140,700 . Its metropolitan area had 409,558 inhabitants at the 1999 census. It is the prefecture of the Puy-de-Dôme department... |
France | Marguerite Périer | Scientific | 8 | 8 x 10 | Marguerite (1646–1733) was Pascal's goddaughter. |
| Musée Henri Lecoq Clermont-Ferrand |
France | Chevalier | Accounting | 5 | 3 x 10 + 20 + 12 | This is the only known machine that came with a box. This is the smallest machine. Was it meant to be portable? |
| Mathematisch-Physikalischer salon, Dresden Dresden Dresden is the capital city of the Free State of Saxony in Germany. It is situated in a valley on the River Elbe, near the Czech border. The Dresden conurbation is part of the Saxon Triangle metropolitan area.... |
Germany | Queen of Poland | Accounting | 10 | 8 x 10 + 20 + 12 | The second wheel from the right has a wheel with 10 spokes contained in a fixed wheel with 20 segments. This could be attributed to a bad restoration. |
| Léon Parcé collection | France | Surveying | 8 | 5 x 10 + 6 + 12 + 12 | This machine was bought as a broken music box in a French antique shop en 1942. | |
| IBM IBM International Business Machines Corporation or IBM is an American multinational technology and consulting corporation headquartered in Armonk, New York, United States. IBM manufactures and sells computer hardware and software, and it offers infrastructure, hosting and consulting services in areas... collection |
USA | Accounting | 8 | 6 x 10 + 20 + 12 |
User interface
Overview
The calculator had spoked metal wheel dials, with the digit 9 through 0 displayed clockwise around the circumference of each wheel (for a decimal wheel). To input a digit, the user placed a stylus in the corresponding space between the spokes, and turned the dial until a metal stop at the bottom was reached, similar to the way a rotary telephone dialRotary dial
The rotary dial is a device mounted on or in a telephone or switchboard that is designed to send electrical pulses, known as pulse dialing, corresponding to the number dialed. The early form of the rotary dial used lugs on a finger plate instead of holes. Almon Brown Strowger filed the first patent...
is used. This would display the number in the boxes at the top of the calculator. Then, one would simply redial the second number to be added, causing the sum of both numbers to appear in boxes at the top. Since the gears of the calculator only rotated in one direction, negative numbers could not be directly summed. To subtract one number from another, the method of nines' complement was used. For all of the numbers inscribed on the result cylinders, their complements (in the given base) were written above them, but only one type could be seen at a time. By moving an horizontal bar up and down across the machine, the user could either display all of the direct numbers or all of their complements.
Input wheel
For a 10 digit wheel (N), the fixed outside wheel is numbered from 0 to 9 (N-1). The numbers are inscribed in a decreasing manner clockwise going from the bottom left to the bottom right of the stopping lever. To add a 5, one must insert a stylus in between the spokes that surround the number 5 and rotate the wheel clockwise all the way to the stopping lever. The number displayed on the corresponding display register will be increased by 5 and, if a carry transfer takes place, the display register to the left of it will be increased by 1. To add fifty, use the tens input wheel (second dial from the right on a decimal machine), to add 500, use the hundreds input wheel, etc...Marks on two adjacent spokes
On all the wheels of all the known machines, except for the machine tardive, two adjacent spokes are marked ; these marks differ from machine to machine, on the wheel pictured on the right, they are drilled dots, on the surveying machine they are carved, some are just scratches or marks made with a bit of varnish, some were even marked with little pieces of paper.These marks are used to set the corresponding cylinder to its maximum number, ready to be re-zeroed. To do so, the operator must insert the stylus in between these two spokes and turn the wheel all the way to the stopping lever. This works because each wheel is directly linked to its corresponding display cylinder (it automatically turns by one during a carry operation) ; to mark the spokes during manufacturing, one can move the cylinder so that its highest number is displayed and then mark the spoke under the stopping lever and the one to the right of it.
Inner wheel of complements
Four of the known machines have inner wheels of complements. They are mounted at the center of each spoked metal wheel and turn with it. The wheel displayed above has an inner wheel of complements but the numbers written on it are barely visible. On a decimal machine, the digits 0 through 9 are carved clockwise, each digit is positioned in between two spokes so that the operator can directly inscribe its value in the window of complements by positioning his stylus in between them and turning the wheel clockwise all the way to the stopping lever. The marks on two adjacent spokes surround the digit 0 inscribed on this wheel.Quotient wheel
On four of the known machines, above each wheel, a small quotient wheel is mounted on the display bar. These quotient wheel, which are set by the operator, have numbers from 1 to 10 inscribed clockwise on their peripheries (even above a non decimal wheel). Quotient wheels seem to have been used during a division to memorize the number of time the divisor was subtracted at each given index.The sautoir
The sautoir is the center piece of the pascaline's carry mechanism. In his "Avis nécessaire...", Pascal wrote:A machine with 10,000 wheels would work as well as a machine with two wheels because each wheel is independent from the other. When it is time to propagate a carry, the sautoir, on the sole influence of gravity, is thrown toward the next wheel without any contact between the wheels. During its free fall the sautoir behaves like an acrobat jumping from one trapeze to the next without the trapezes touching each other (sautoir comes from the french verb sauter which means to jump). All the wheels (including gears and sautoir) have therefore the same size and weight independently of the capacity of the machine.
Pascal used gravity to arm the sautoirs. One must turn the wheel five steps from 4 to 9 in order to fully arm a sautoir, but the carry transfer will only move the next wheel one step. Therefore there is a lot of extra energy built up during the arming of a sautoir.
All the sautoirs are armed by either an operator input or a carry forward. To re-zero a 10,000 wheel machine, if it existed, the operator would have to set every wheel to its maximum and then add a 1 to the "unit" wheel. The carry would turn every input wheel one by one in a very rapid Domino effect
Domino effect
The domino effect is a chain reaction that occurs when a small change causes a similar change nearby, which then will cause another similar change, and so on in linear sequence. The term is best known as a mechanical effect, and is used as an analogy to a falling row of dominoes...
fashion and all the display registers would be reset.
The three phases of a carry transmission
The animation on the right shows the three phases of a carry transmission.- The first phase happens when the display register goes from 4 to 9. The two carry pins (one after the other) lift the sautoir pushing on its protruding part marked (3,4,5). At the same time the is pulled up, using a pin on the next wheel as guidance, but without effect on this wheel because of the .
- The second phase starts when the display register goes from 9 to 0. The pawl passes its guiding pin and its positions it above this pin ready to push on it. The sautoir keeps on moving up and suddenly the second carry pin drops it. The sautoir is falling of its own weight.
- The pushes the pin on the next wheel and starts turning it. The is moved to the next space. The operation stops when the protruding hits the .
- During the first phase, the active wheel touches the one that will receive the carry through the sautoir, but it never moves it or modifies it and therefore the status of the receiving wheel has no impact whatsoever on the active wheel.
- During the second phase, the sautoir and the two wheels are completely disconnected.
- During the third phase the sautoir, which no longer touches the active wheel, adds one to the receiving wheel.
Principle
The Pascaline is a direct adding machine (it doesn't have a crank handle) so the value of a number is added to the accumulator as it is being dialed in. By moving a display bar, the operator can either see the number stored in the calculator or the complement of its value. Subtractions are performed like additions by using some properties of 9's complement arithmetic.9's complement
The 9's complement of any one digit decimal number d is 9 - d. So the 9's complement of 4 is 5 and the 9's complement of 9 is 0. Similarly the 11's complement of 3 is 8.In a decimal machine with n dials the 9's complement of a number A is:
- CP(A)= 10n - 1 - A
and therefore the 9's complement of (A - B) is:
- CP(A - B)= 10n -1 - (A - B) = 10n -1 - A + B = CP(A) + B
- CP(A - B)= CP(A) + B
In other words, the 9's complement of the difference of two numbers is equal to the sum of the 9's complement of the minuend added to the subtrahend. The same principle is valid and can be used with numbers composed of digits of various bases (base 6, 12, 20) like in the surveying or the accounting machines.
This can also be extended to:
- CP(A - B - C - D)= CP(A) + B + C + D
This principle applied to the pascaline:
| CP(A): | First the complement of the minuend is entered. The operator can either use the inner wheels of complements or dial the complement of the minuend directly. The display bar is shifted to show the complement's window so that the operator sees the direct number displayed because . |
| B: | Then the second number is dialed in and adds its value to the accumulator. |
| The result (A - B) is displayed in the complement window because . The last step can be repeated as long as the subtrahend is smaller than the minuend displayed in the accumulator,. | |
Resetting the machine
The machine has to be re-zeroed before each new operation.To reset his machine, the operator has to set all the wheels to their maximum, using the marks on two adjacent spokes, and then add 1 to the rightmost wheel.
The method of re-zeroing that Pascal chose, which propagates a carry right through the machine, is the most demanding task for a mechanical calculator and proves, before each operation, that the machine is fully functional.
This is a testament to the quality of the Pascaline because none of the 18th century criticisms of the machine mentioned a problem with the carry mechanism and yet this feature was fully tested on all the machines, by their resets, all the time.
| Re-zero | Set all the wheels to their maximum. Every single wheel is ready for a carry transfer. | |||
| 0 | 0 | 0 | 0 | 0 |
| 9 | 9 | 9 | 9 | 9 |
Addition
Additions are performed with the display bar moved closest to the edge of the machine, showing the direct value of the accumulator.After re-zeroing the machine, numbers are dialed in one after the other.
The following table shows all the steps required to compute: 12,345 + 56,789 = 69,134
| Addition | The machine is at zero, the operator enters 12,345. | |||
| 8 | 7 | 6 | 5 | 4 |
| 1 | 2 | 3 | 4 | 5 |
Subtraction
Subtractions are performed with the display bar moved closest to the center of the machine showing the complement value of the accumulator.The accumulator contains CP( A ) during the first step and CP( A - B) after adding B. In displaying that data in the complement window, the operator sees CP( CP( A)) which is A and then CP(CP( A - B )) which is (A - B). It feels like an addition. The only two differences in between an addition and a subtraction are the position of the display bar and the way the first number is entered (direct versus complement).
The following table shows all the steps required to compute: 54,321 - 12,345 = 41,976
| Change display space | Move the display bar down to uncover the complement part of each result cylinder. From this point on, every number dialed into the machine adds its value to the accumulator and therefore decreases the total displayed in the complement window. | |||
| 9 | 9 | 9 | 9 | 9 |
| 0 | 0 | 0 | 0 | 0 |

