
Pieri's formula
Encyclopedia
In mathematics, Pieri's formula, named after Mario Pieri
, describes the product of a Schubert cycle by a special Schubert cycle in the Schubert calculus
, or the product of a Schur polynomial
by a complete symmetric function.
In terms of Schur functions sλ indexed by partitions
λ, it states that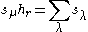
where hr is a complete homogeneous symmetric polynomial
and the sum is over all partitions λ obtained from μ by adding r elements, no two in the same column.
Pieri's formula implies Giambelli's formula
. The Littlewood–Richardson rule
is a generalization of Pieri's formula
giving the product of any two Schur functions. Monk's formula
is an analogue of Pieri's formula for flag manifolds.
Mario Pieri
Mario Pieri was an Italian mathematician who is known for his work on foundations of geometry.Pieri was born in Lucca, Italy, the son of Pellegrino Pieri and Ermina Luporini. Pellegrino was a lawyer. Pieri began his higher education at University of Bologna where he drew the attention of Salvatore...
, describes the product of a Schubert cycle by a special Schubert cycle in the Schubert calculus
Schubert calculus
In mathematics, Schubert calculus is a branch of algebraic geometry introduced in the nineteenth century by Hermann Schubert, in order to solve various counting problems of projective geometry...
, or the product of a Schur polynomial
Schur polynomial
In mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of...
by a complete symmetric function.
In terms of Schur functions sλ indexed by partitions
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
λ, it states that
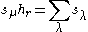
where hr is a complete homogeneous symmetric polynomial
Complete homogeneous symmetric polynomial
In mathematics, specifically in algebraic combinatorics and commutative algebra, the complete homogeneous symmetric polynomials are a specific kind of symmetric polynomials...
and the sum is over all partitions λ obtained from μ by adding r elements, no two in the same column.
Pieri's formula implies Giambelli's formula
Giambelli's formula
In mathematics, Giambelli's formula, named after Giovanni Giambelli, expresses Schubert classes in terms of special Schubert classes, or Schur functions in terms of complete symmetric functions....
. The Littlewood–Richardson rule
Littlewood–Richardson rule
In mathematics, the Littlewood–Richardson rule is a combinatorial description of the coefficients that arise when decomposing a product of two Schur functions as a linear combination of other Schur functions. These coefficients are natural numbers, which the Littlewood–Richardson rule describes as...
is a generalization of Pieri's formula
giving the product of any two Schur functions. Monk's formula
Monk's formula
In mathematics, Monk's formula, found by , is an analogue of Pieri's formula that describes the product of a linear Schubert polynomial by a Schubert polynomial. Equivalently, it describes the product of a special Schubert cycle by a Schubert cycle in the cohomology of a flag manifold.-References:...
is an analogue of Pieri's formula for flag manifolds.

