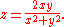Plücker’s conoid
Encyclopedia
In geometry
, the Plücker’s conoid is a ruled surface
named after the German mathematician Julius Plücker
. It is also called a cylindroid
or conical wedge.
The Plücker’s conoid is defined by the function of two variables:
By using cylindrical coordinates in space, we can write the above functon into parametric equations
Thus the Plücker’s conoid is a right conoid
, which can be obtained by rotating a horizontal line about the z-axis with the oscillatory motion (with period 2π) along the segment [−1, 1] of the axis (Figure 4).
A generalization of the Plücker’s conoid is given by the parametric equations
where n denotes the number of folds in the surface. The difference is that the period of the oscillatory motion along the z-axis is 2π/n. (Figure 5 for n = 3)
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Plücker’s conoid is a ruled surface
Ruled surface
In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. The most familiar examples are the plane and the curved surface of a cylinder or cone...
named after the German mathematician Julius Plücker
Julius Plücker
Julius Plücker was a German mathematician and physicist. He made fundamental contributions to the field of analytical geometry and was a pioneer in the investigations of cathode rays that led eventually to the discovery of the electron. He also vastly extended the study of Lamé curves.- Early...
. It is also called a cylindroid
Cylindroid
A cylindroid is a cylinder that has an elliptical cross-section. See also Plücker’s conoid....
or conical wedge.
The Plücker’s conoid is defined by the function of two variables:
By using cylindrical coordinates in space, we can write the above functon into parametric equations
Thus the Plücker’s conoid is a right conoid
Right conoid
In geometry, a right conoid is a ruled surface generated by a family of straight lines that all intersect perpendicularly a fixed straight line, called the axis of the right conoid....
, which can be obtained by rotating a horizontal line about the z-axis with the oscillatory motion (with period 2π) along the segment [−1, 1] of the axis (Figure 4).
A generalization of the Plücker’s conoid is given by the parametric equations
where n denotes the number of folds in the surface. The difference is that the period of the oscillatory motion along the z-axis is 2π/n. (Figure 5 for n = 3)
External links
- Plücker’s conoid from MathWorld