Pompeiu's theorem
Encyclopedia
Pompeiu's theorem is a result of plane geometry
, discovered by the Romanian mathematician Dimitrie Pompeiu
. The theorem is quite simple, but not classical. It states the following:
The proof is quick. Consider a rotation of 60° about the point C. Assume A maps to B, and B maps to B' . Then we have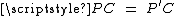 
, and 
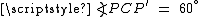. Hence triangle PCP ' is equilateral and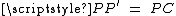 
. It is obvious that 
. Thus, triangle PBP ' has sides equal to PA, PB, and PC and the proof by construction is complete.
Further investigations reveal that if P is not in the interior of the triangle, but rather on the circumcircle, then PA, PB, PC form a degenerate triangle, with the largest being equal to the sum of the others.
Plane geometry
In mathematics, plane geometry may refer to:*Euclidean plane geometry, the geometry of plane figures,*geometry of a plane,or sometimes:*geometry of a projective plane, most commonly the real projective plane but possibly the complex projective plane, Fano plane or others;*geometry of the hyperbolic...
, discovered by the Romanian mathematician Dimitrie Pompeiu
Dimitrie Pompeiu
-Biography:After studying in Dorohoi and Bucharest, he went to France, where he studied mathematics at the University of Paris . He obtained a Ph.D. degree in mathematics in 1905 with a thesis, On the continuity of complex variable functions, written under the direction of Henri Poincaré...
. The theorem is quite simple, but not classical. It states the following:
- Given an equilateral triangle ABC in the plane, and a point P in the plane of the triangle ABC, the lengths PA, PB, and PC form the sides of a (maybe, degenerate) triangle.
The proof is quick. Consider a rotation of 60° about the point C. Assume A maps to B, and B maps to B
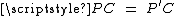, and 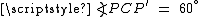. Hence triangle PCP 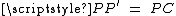. It is obvious that . Thus, triangle PBP Further investigations reveal that if P is not in the interior of the triangle, but rather on the circumcircle, then PA, PB, PC form a degenerate triangle, with the largest being equal to the sum of the others.