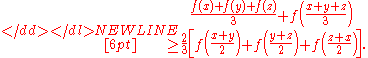In convex analysis

Convex analysis

Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....

, Popoviciu's inequality is an inequality about convex function

Convex function

In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...

s. It is similar to Jensen's inequality

Jensen's inequality

In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...

 and was found in 1965 by Tiberiu Popoviciu, a Romanian mathematician. It states:

Let ƒ be a function from an interval to . If ƒ is convex

Convex function

In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...

, then for any three points from ,

If a function ƒ is continuous, then it is convex if and only if the above inequality holds for all x, y, z from . When ƒ is strictly convex, the inequality is strict except for x = y = z.

It can be generalised to any finite number n of points instead of 3, taken on the right-hand side k at a time instead of 2 at a time:

Let ƒ be a continuous function from an interval to . Then ƒ is convex

Convex function

In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...

if and only if, for any integers n and k where n ≥ 3 and , and any points from ,

Popoviciu's inequality can also be generalised to a weighted inequality.