Riesz's lemma
Encyclopedia
Riesz's lemma is a lemma
in functional analysis
. It specifies (often easy to check) conditions which guarantee that a subspace
in a normed linear space is dense
.
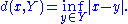
Riesz's lemma reads as follows:
In other words, for every proper closed subspace Y, one can always find a vector x on the unit sphere of X such that d(x, Y) is less than and arbitrarily close to 1.
Proof: A simple proof can be sketched as follows. Suppose Y is not dense in X, therefore the closure of Y, denoted by Y' , is a proper subspace of X. Take an element x not in Y' , then we have
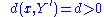
So, for any k > 1, there exists y0 in Y' such that
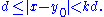
Consider the vector z = x - y0. We can calculate directly
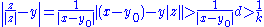
for any y in Y. Choosing k arbitrarily close to 1 finishes the proof.
On the other hand, the example of the space
of all bounded sequences shows that the lemma does not hold for k = 1.
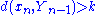for a constant 0 < k < 1, where Yn-1 is the linear span of {x1 ... xn-1}.
Clearly {xn} contains no convergent subsequence and the noncompactness of the unit ball follows.
The converse of this, in a more general setting, is also true. If a topological vector space
X is locally compact, then it is finite dimensional. Therefore local compactness characterizes finite-dimensionality. This classical result is also attributed to Riesz. A short proof can be sketched as follows: let C be a compact neighborhood of 0 ∈ X. By compactness, there is c1 ... cn ∈ C such that
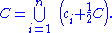
We claim that the finite dimensional subspace Y spanned by {ci}, or equivalently, its closure, is X. Since scalar multiplication is continuous, its enough to show C ⊂ Y. Now, by induction,
for every m. But compact sets are bounded
, so C lies in the closure of Y. This proves the result.
acting on a Banach space are similar to those of matrices. Riesz's lemma is essential in establishing this fact.
Riesz's lemma guarantees that any infinite-dimensional normed space contains a sequence of unit vectors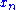
with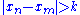 
for 0 < k < 1. This is useful in showing the non-existence of certain measures
on infinite-dimensional Banach space
s.
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. It specifies (often easy to check) conditions which guarantee that a subspace
Subspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
in a normed linear space is dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
.
The result
Before stating the result, we fix some notation. Let X be a normed linear space with norm |·| and x be an element of X. Let Y be a subspace in X. The distance between an element x and Y is defined by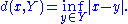Riesz's lemma reads as follows:
- Let X be a normed linear space and Y be a subspace in X. If there exists 0 < r < 1 such that for every x ∈ X with |x| =1, one has d(x, Y) < r, then Y is dense in X.
In other words, for every proper closed subspace Y, one can always find a vector x on the unit sphere of X such that d(x, Y) is less than and arbitrarily close to 1.
Proof: A simple proof can be sketched as follows. Suppose Y is not dense in X, therefore the closure of Y, denoted by Y' , is a proper subspace of X. Take an element x not in Y' , then we have
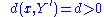
So, for any k > 1, there exists y0 in Y' such that
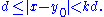
Consider the vector z = x - y0. We can calculate directly
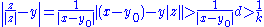
for any y in Y. Choosing k arbitrarily close to 1 finishes the proof.
Note
For the finite dimensional case, equality can be achieved. In other words, there exists x of unit norm such that d(x, Y) is 1. When dimension of X is finite, the unit ball B ⊂ X is compact. Also, the distance function d(· , Y) is continuous. Therefore its image on the unit ball B must be a compact subset of the real line, and this proves the claim.On the other hand, the example of the space
of all bounded sequences shows that the lemma does not hold for k = 1.Converse
Riesz's lemma can be applied directly to show that the unit ball of an infinite-dimensional normed space X is never compact: Take an element x1 from the unit sphere. Pick xn from the unit sphere such that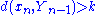 for a constant 0 < k < 1, where Yn-1 is the linear span of {x1 ... xn-1}.Clearly {xn} contains no convergent subsequence and the noncompactness of the unit ball follows.
The converse of this, in a more general setting, is also true. If a topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
X is locally compact, then it is finite dimensional. Therefore local compactness characterizes finite-dimensionality. This classical result is also attributed to Riesz. A short proof can be sketched as follows: let C be a compact neighborhood of 0 ∈ X. By compactness, there is c1 ... cn ∈ C such that
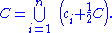
We claim that the finite dimensional subspace Y spanned by {ci}, or equivalently, its closure, is X. Since scalar multiplication is continuous, its enough to show C ⊂ Y. Now, by induction,
for every m. But compact sets are bounded
Bounded set (topological vector space)
In functional analysis and related areas of mathematics, a set in a topological vector space is called bounded or von Neumann bounded, if every neighborhood of the zero vector can be inflated to include the set...
, so C lies in the closure of Y. This proves the result.
Some consequences
The spectral properties of compact operatorsSpectral theory of compact operators
In functional analysis, compact operators are linear operators that map bounded sets to precompact sets. The set of compact operators acting on a Hilbert space H is the closure of the set of finite rank operators in the uniform operator topology. In general, operators on infinite dimensional spaces...
acting on a Banach space are similar to those of matrices. Riesz's lemma is essential in establishing this fact.
Riesz's lemma guarantees that any infinite-dimensional normed space contains a sequence of unit vectors
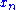with 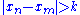for 0 < k < 1. This is useful in showing the non-existence of certain measuresMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on infinite-dimensional Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s.