
Rodrigues' formula
Encyclopedia
In mathematics, Rodrigues's formula (formerly called the Ivory–Jacobi formula) is a formula for Legendre polynomials independently introduced by , and . The name "Rodrigues formula" was introduced by Heine in 1878, after Hermite pointed out in 1865 that Rodrigues was the first to discover it, and is also used for generalizations to other orthogonal polynomials
.
describes the history of the Rodrigues formula in detail.
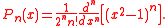
A similar formula holds for many other sequences of orthogonal polynomials pn:
and these generalizations are also called Rodrigues' formula.
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
.
describes the history of the Rodrigues formula in detail.
Statement
Rodrigues stated his formula for Legendre polynomials Pn: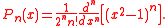
A similar formula holds for many other sequences of orthogonal polynomials pn:

and these generalizations are also called Rodrigues' formula.

