Rouché–Capelli theorem
Encyclopedia
–Capelli
theorem is the theorem in linear algebra
that allows computing the number of solutions in a system of linear equations given the ranks of its augmented matrix
and coefficient matrix
. The theorem is known as Kronecker–Capelli theorem in Russia, Rouché–Capelli theorem in Italy, Rouché–Fontené theorem in France and Rouché–Frobenius
theorem in Spain.
variables has a solution if and only if
the rank
of its coefficient matrix
A is equal to the rank of its augmented matrix
[A|b]. If there are solutions, they form an affine subspace of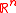
of dimension n − rank(A). In particular:
Alfredo Capelli
Alfredo Capelli was an Italian mathematician who discovered Capelli's identity.Capelli graduated from the University of Rome in 1877, and moved to the University of Pavia where he worked as an assistant for Felice Casorati...
theorem is the theorem in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
that allows computing the number of solutions in a system of linear equations given the ranks of its augmented matrix
Augmented matrix
In linear algebra, an augmented matrix is a matrix obtained by appending the columns of two given matrices, usually for the purpose of performing the same elementary row operations on each of the given matrices.Given the matrices A and B, where:A =...
and coefficient matrix
Coefficient matrix
In linear algebra, the coefficient matrix refers to a matrix consisting of the coefficients of the variables in a set of linear equations.-Example:...
. The theorem is known as Kronecker–Capelli theorem in Russia, Rouché–Capelli theorem in Italy, Rouché–Fontené theorem in France and Rouché–Frobenius
Ferdinand Georg Frobenius
Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
theorem in Spain.
Formal statement
A system of linear equations with variables has a solution if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of its coefficient matrix
Coefficient matrix
In linear algebra, the coefficient matrix refers to a matrix consisting of the coefficients of the variables in a set of linear equations.-Example:...
A is equal to the rank of its augmented matrix
Augmented matrix
In linear algebra, an augmented matrix is a matrix obtained by appending the columns of two given matrices, usually for the purpose of performing the same elementary row operations on each of the given matrices.Given the matrices A and B, where:A =...
[A|b]. If there are solutions, they form an affine subspace of
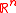of dimension n − rank(A). In particular:
- if n = rank(A), the solution is unique,
- otherwise there are infinite number of solutions.