Saint-Venant's principle
Encyclopedia
Saint-Venant's principle, named after the French elasticity theorist Jean Claude Barré de Saint-Venant
can be stated as saying that
The original statement was published in French by Saint-Venant in 1855. Although this informal statement of the principle is well known among mechanical engineers, more recent mathematical literature gives a rigorous interpretation in the context of partial differential equations. An early such intepratation was made by von Mises in 1945
The Saint-Venant's principle allows elasticians to replace complicated stress distributions or weak boundary conditions into ones that are easier to solve, as long as that boundary is geometrically short. Quite analogous to the electrostatics
, where the electric field
due to the i-th moment of the load ( with 0th being the net charge, 1st the dipole
, 2nd the quadrupole
) decays as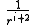
over space, Saint-Venant's principle states that high order momentum of mechanical load ( moment with order higher than torque
) decays so fast that they never need to be considered for regions far from the short boundary. Therefore, the Saint-Venant's principle can be regarded as a statement on the asymptotic behavior of the Green's function
by a point-load.
Adhémar Jean Claude Barré de Saint-Venant
Adhémar Jean Claude Barré de Saint-Venant was a mechanician and mathematician who contributed to early stress analysis and also developed the one-dimensional unsteady open channel flow shallow water equations or Saint-Venant equations that are a fundamental set of equations used in modern...
can be stated as saying that
- "... the difference between the effects of two different but statically equivalent load becomes very small at sufficiently large distances from load."
The original statement was published in French by Saint-Venant in 1855. Although this informal statement of the principle is well known among mechanical engineers, more recent mathematical literature gives a rigorous interpretation in the context of partial differential equations. An early such intepratation was made by von Mises in 1945
The Saint-Venant's principle allows elasticians to replace complicated stress distributions or weak boundary conditions into ones that are easier to solve, as long as that boundary is geometrically short. Quite analogous to the electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
, where the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
due to the i-th moment of the load ( with 0th being the net charge, 1st the dipole
Dipole
In physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
, 2nd the quadrupole
Quadrupole
A quadrupole or quadrapole is one of a sequence of configurations of—for example—electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.-Mathematical...
) decays as
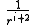over space, Saint-Venant's principle states that high order momentum of mechanical load ( moment with order higher than torqueTorque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
) decays so fast that they never need to be considered for regions far from the short boundary. Therefore, the Saint-Venant's principle can be regarded as a statement on the asymptotic behavior of the Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
by a point-load.