Schanuel's lemma
Encyclopedia
In mathematics
, especially in the area of algebra
known as module theory, Schanuel's lemma, namead after Stephen Schanuel
, allows one to compare how far modules depart from being projective
. It is useful in defining the Heller operator in the stable category, and in giving elementary descriptions of dimension shifting.
If 0 → K → P → M → 0 and 0 → K → P ' → M → 0 are short exact sequences of R-modules and P and P ' are projective, then K ⊕ P ' is isomorphic
to K ' ⊕ P.
The map π : X → P, where π is defined as the projection of the first coordinate of X into P, is surjective. Since φ is surjective, for any p
X, one may find a q 
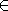P ' such that φ(p) = φ '(q). This gives (p,q) 
X with π (p,q) = p. Now examine the kernel
of the map π :
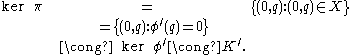
We may conclude that there is a short exact sequence
Since P is projective this sequence splits, so X ≅ K ' ⊕ P . Similarly, we can write another map π : X → P ', and the same argument as above shows that there is another short exact sequence
and so X ≅ P ' ⊕ K. Combining the two equivalences for X gives the desired result.
discovered the argument in Irving Kaplansky
's homological algebra
course at the University of Chicago
in Autumn of 1958. Kaplansky writes:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
known as module theory, Schanuel's lemma, namead after Stephen Schanuel
Stephen Schanuel
Stephen H. Schanuel is an American mathematician working in the fields of abstract algebra and number theory, more specifically category theory and measure theory....
, allows one to compare how far modules depart from being projective
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
. It is useful in defining the Heller operator in the stable category, and in giving elementary descriptions of dimension shifting.
Statement
Schanuel's lemma is the following statement:If 0 → K → P → M → 0 and 0 → K → P ' → M → 0 are short exact sequences of R-modules and P and P ' are projective, then K ⊕ P ' is isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to K ' ⊕ P.
Proof
Define the following submodule of P ⊕ P ', where φ : P → M and φ' : P ' → M:The map π : X → P, where π is defined as the projection of the first coordinate of X into P, is surjective. Since φ is surjective, for any p
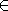X, one may find a q P ' such that φ(p) = φ '(q). This gives (p,q) X with π (p,q) = p. Now examine the kernelKernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of the map π :
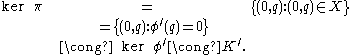
We may conclude that there is a short exact sequence
Since P is projective this sequence splits, so X ≅ K ' ⊕ P . Similarly, we can write another map π : X → P ', and the same argument as above shows that there is another short exact sequence
and so X ≅ P ' ⊕ K. Combining the two equivalences for X gives the desired result.
Origins
Stephen SchanuelStephen Schanuel
Stephen H. Schanuel is an American mathematician working in the fields of abstract algebra and number theory, more specifically category theory and measure theory....
discovered the argument in Irving Kaplansky
Irving Kaplansky
Irving Kaplansky was a Canadian mathematician.-Biography:He was born in Toronto, Ontario, Canada, after his parents emigrated from Poland and attended the University of Toronto as an undergraduate. After receiving his Ph.D...
's homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
course at the University of Chicago
University of Chicago
The University of Chicago is a private research university in Chicago, Illinois, USA. It was founded by the American Baptist Education Society with a donation from oil magnate and philanthropist John D. Rockefeller and incorporated in 1890...
in Autumn of 1958. Kaplansky writes:
- Early in the course I formed a one-step projective resolution of a module, and remarked that if the kernel was projective in one resolution it was projective in all. I added that, although the statement was so simple and straightforward, it would be a while before we proved it. Steve Shanuel spoke up and told me and the class that it was quite easy, and thereupon sketched what has come to be known as "Schanuel's lemma."