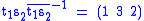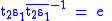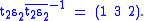Schreier's subgroup lemma
Encyclopedia
Schreier's subgroup lemma is a theorem
in group theory
used in the Schreier–Sims algorithm and also for finding a presentation
of a subgroup
.
is a subgroup
of
, which is finitely generated with generating set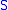 
, that is, G = <S>.
Let
be a right transversal
of
in 
.
We make the definition that given
∈
, 
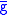is the chosen representative in the transversal 
of the coset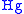 
, that is,
Then
is generated by the set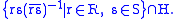
, Z3 is a subgroup of the symmetric group
S3. Now,
where
is the identity permutation. Note S3 = < { s1=(1 2), s2=(1 2 3) } >.
Z3 has just two cosets, Z3 and S3 \ Z3, so we select the transversal { t1=e, t2=(1 2) }, and we have
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
used in the Schreier–Sims algorithm and also for finding a presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
of a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
.
Definition
Suppose is a subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of
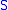, which is finitely generated with generating set , that is, G = <S>.Let
be a right transversalTransversal
In geometry , when two coplanar lines exist such that a third coplanar line passes thru both lines. This third line is named the Transversal....
of
in .We make the definition that given
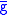∈, is the chosen representative in the transversal of the coset 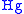, that is,Then
is generated by the set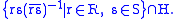Example
Let us establish the evident fact that the group Z3=Z/3Z is indeed cyclic. Via Cayley's theoremCayley's theorem
In group theory, Cayley's theorem, named in honor of Arthur Cayley, states that every group G is isomorphic to a subgroup of the symmetric group acting on G...
, Z3 is a subgroup of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
S3. Now,
where
is the identity permutation. Note S3 = < { s1=(1 2), s2=(1 2 3) } >.Z3 has just two cosets, Z3 and S3 \ Z3, so we select the transversal { t1=e, t2=(1 2) }, and we have
-
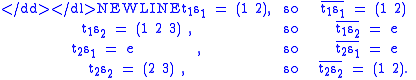
Finally,
Thus, by Schreier's subgroup lemma, { e, (1 3 2) } generates Z3, but having the identity in the generating set is redundant, so we can remove it to obtain another generating set for Z3, { (1 3 2) } (as expected). -
