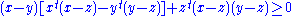Schur's inequality
Encyclopedia
In mathematics
, Schur's inequality, named after Issai Schur
,
establishes that for all non-negative real number
s
x, y, z and a positive number t,
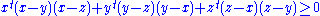
with equality if and only if x = y = z or two of them are equal and the other is zero. When t is an even positive integer
, the inequality holds for all real numbers x, y and z.
When , the following well-known special case can be derived:
, the following well-known special case can be derived: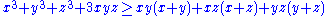
 we may assume without loss of generality that
we may assume without loss of generality that 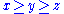 . Then the inequality
. Then the inequality
clearly holds, since every term on the left-hand side of the equation is non-negative. This rearranges to Schur's inequality.
of Schur's inequality is the following:
Suppose a,b,c are positive real numbers. If the triples (a,b,c) and (x,y,z) are similarly sorted, then the following inequality holds:
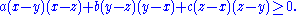
In 2007, Romania
n mathematician Valentin Vornicu
showed that a yet further generalized form of Schur's inequality holds:
Consider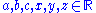 , where
, where 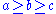 , and either
, and either 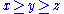 or
or 
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Schur's inequality, named after Issai Schur
Issai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
,
establishes that for all non-negative real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s
x, y, z and a positive number t,
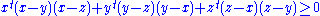
with equality if and only if x = y = z or two of them are equal and the other is zero. When t is an even positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, the inequality holds for all real numbers x, y and z.
When
 , the following well-known special case can be derived:
, the following well-known special case can be derived: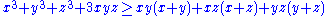
Proof
Since the inequality is symmetric in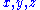 we may assume without loss of generality that
we may assume without loss of generality that 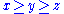 . Then the inequality
. Then the inequalityclearly holds, since every term on the left-hand side of the equation is non-negative. This rearranges to Schur's inequality.
Extension
A generalizationGeneralization
A generalization of a concept is an extension of the concept to less-specific criteria. It is a foundational element of logic and human reasoning. Generalizations posit the existence of a domain or set of elements, as well as one or more common characteristics shared by those elements. As such, it...
of Schur's inequality is the following:
Suppose a,b,c are positive real numbers. If the triples (a,b,c) and (x,y,z) are similarly sorted, then the following inequality holds:
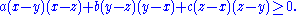
In 2007, Romania
Romania
Romania is a country located at the crossroads of Central and Southeastern Europe, on the Lower Danube, within and outside the Carpathian arch, bordering on the Black Sea...
n mathematician Valentin Vornicu
Valentin Vornicu
Valentin Vornicu is the founder of MathLinks. He is also the previous webmaster of the Art of Problem Solving.-Mathematics and education:Valentin Vornicu was a part of the Romanian team for the International Mathematics Olympiad in 2001 and 2002. In 2002 he obtained a Bronze Medal at the IMO...
showed that a yet further generalized form of Schur's inequality holds:
Consider
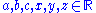 , where
, where 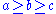 , and either
, and either 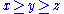 or
or