
Shamir's Secret Sharing
Encyclopedia
Shamir's Secret Sharing is an algorithm
in cryptography
. It is a form of secret sharing
, where a secret is divided into parts, giving each participant its own unique part, where some of the parts or all of them are needed in order to reconstruct the secret.
Counting on all participants to combine together the secret might be impractical, and therefore sometimes the threshold scheme is used where any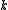 of the parts are sufficient to reconstruct the original secret.
of the parts are sufficient to reconstruct the original secret.
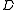 (e.g., the safe combination) into
(e.g., the safe combination) into 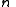 pieces
pieces 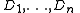 in such a way that:
in such a way that:
This scheme is called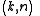 threshold scheme.
threshold scheme.
If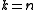 then all participants are required to reconstruct the secret.
then all participants are required to reconstruct the secret.
's threshold scheme is that 2 point
s are sufficient to define a line
, 3 points are sufficient to define a parabola
, 4 points to define a cubic curve
and so forth.
That is, it takes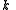 points to define a polynomial
points to define a polynomial
of degree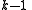 .
.
Suppose we want to use a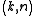 threshold scheme to share our secret
threshold scheme to share our secret 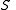 , without loss of generality assumed to be an element in a finite field
, without loss of generality assumed to be an element in a finite field
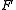 .
.
Choose at random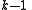 coefficients
coefficients 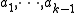 in
in 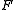 , and let
, and let 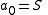 . Build the polynomial
. Build the polynomial 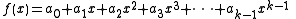 . Let us construct any
. Let us construct any 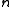 points out of it, for instance set
points out of it, for instance set 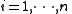 to retrieve
to retrieve 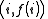 . Every participant is given a point (a pair of input to the polynomial and output).
. Every participant is given a point (a pair of input to the polynomial and output).
Given any subset of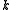 of these pairs, we can find the coefficients of the polynomial using interpolation
of these pairs, we can find the coefficients of the polynomial using interpolation
and the secret is the constant term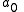 .
.
. Therefore the example below does not provide perfect secrecy, and is not a true example of Shamir's scheme.
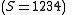 .
.
We wish to divide the secret into 6 parts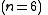 , where any subset of 3 parts
, where any subset of 3 parts 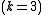 is sufficient to reconstruct the secret. At random we obtain 2 numbers: 166, 94.
is sufficient to reconstruct the secret. At random we obtain 2 numbers: 166, 94.
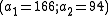
Our polynomial to produce secret shares (points) is therefore:
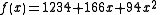
We construct 6 points from the polynomial:
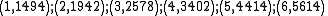
We give each participant a different single point (both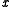 and
and 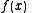 ).
).
Let us consider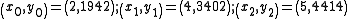 .
.
We will compute Lagrange basis polynomials
:
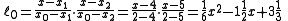
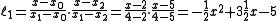
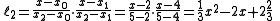
Therefore
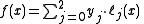
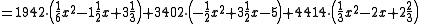
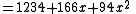
Recall that the secret is the free coefficient, which means that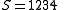 , and we are done.
, and we are done.
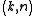 threshold scheme are:
threshold scheme are:
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
. It is a form of secret sharing
Secret sharing
Secret sharing refers to method for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together; individual shares are of no use on their own.More formally, in a...
, where a secret is divided into parts, giving each participant its own unique part, where some of the parts or all of them are needed in order to reconstruct the secret.
Counting on all participants to combine together the secret might be impractical, and therefore sometimes the threshold scheme is used where any
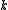 of the parts are sufficient to reconstruct the original secret.
of the parts are sufficient to reconstruct the original secret.Mathematical definition
Formally, our goal is to divide some data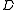 (e.g., the safe combination) into
(e.g., the safe combination) into 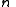 pieces
pieces 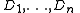 in such a way that:
in such a way that:- Knowledge of any
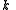 or more
or more 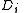 pieces makes
pieces makes 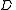 easily computable.
easily computable. - Knowledge of any
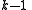 or fewer
or fewer 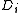 pieces leaves
pieces leaves 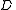 completely undetermined (in the sense that all its possible values are equally likely).
completely undetermined (in the sense that all its possible values are equally likely).
This scheme is called
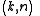 threshold scheme.
threshold scheme.If
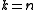 then all participants are required to reconstruct the secret.
then all participants are required to reconstruct the secret.Shamir's secret-sharing scheme
The essential idea of Adi ShamirAdi Shamir
Adi Shamir is an Israeli cryptographer. He is a co-inventor of the RSA algorithm , a co-inventor of the Feige–Fiat–Shamir identification scheme , one of the inventors of differential cryptanalysis and has made numerous contributions to the fields of cryptography and computer...
's threshold scheme is that 2 point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
s are sufficient to define a line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, 3 points are sufficient to define a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, 4 points to define a cubic curve
Cubic function
In mathematics, a cubic function is a function of the formf=ax^3+bx^2+cx+d,\,where a is nonzero; or in other words, a polynomial of degree three. The derivative of a cubic function is a quadratic function...
and so forth.
That is, it takes
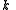 points to define a polynomial
points to define a polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
of degree
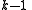 .
.Suppose we want to use a
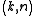 threshold scheme to share our secret
threshold scheme to share our secret 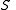 , without loss of generality assumed to be an element in a finite field
, without loss of generality assumed to be an element in a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
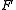 .
.Choose at random
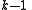 coefficients
coefficients 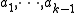 in
in 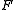 , and let
, and let 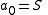 . Build the polynomial
. Build the polynomial 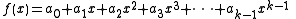 . Let us construct any
. Let us construct any 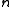 points out of it, for instance set
points out of it, for instance set 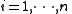 to retrieve
to retrieve 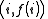 . Every participant is given a point (a pair of input to the polynomial and output).
. Every participant is given a point (a pair of input to the polynomial and output).Given any subset of
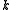 of these pairs, we can find the coefficients of the polynomial using interpolation
of these pairs, we can find the coefficients of the polynomial using interpolationCurve fitting
Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function...
and the secret is the constant term
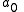 .
.Example
The following example illustrates the basic idea. Note, however, that calculations in the example are done using integer arithmetic rather than using finite field arithmeticFinite field arithmetic
Arithmetic in a finite field is different from standard integer arithmetic. There are a limited number of elements in the finite field; all operations performed in the finite field result in an element within that field....
. Therefore the example below does not provide perfect secrecy, and is not a true example of Shamir's scheme.
Preparation
Suppose that our secret is 1234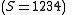 .
.We wish to divide the secret into 6 parts
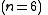 , where any subset of 3 parts
, where any subset of 3 parts 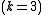 is sufficient to reconstruct the secret. At random we obtain 2 numbers: 166, 94.
is sufficient to reconstruct the secret. At random we obtain 2 numbers: 166, 94.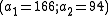
Our polynomial to produce secret shares (points) is therefore:
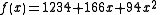
We construct 6 points from the polynomial:
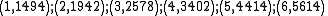
We give each participant a different single point (both
 and
and 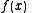 ).
).Reconstruction
In order to reconstruct the secret any 3 points will be enough.Let us consider
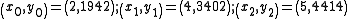 .
.We will compute Lagrange basis polynomials
Lagrange polynomial
In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
:
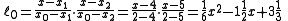
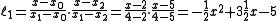
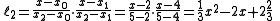
Therefore
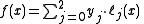
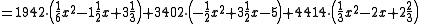
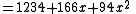
Recall that the secret is the free coefficient, which means that
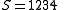 , and we are done.
, and we are done.Properties
Some of the useful properties of Shamir's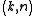 threshold scheme are:
threshold scheme are:
- Secure: Information theoretic securityInformation theoretic securityA cryptosystem is information-theoretically secure if its security derives purely from information theory. That is, it is secure even when the adversary has unlimited computing power. The adversary simply does not have enough information to break the security...
. - Minimal: The size of each piece does not exceed the size of the original data.
- Extensible: When
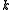 is kept fixed,
is kept fixed, 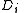 pieces can be dynamically added or deleted without affecting the other pieces.
pieces can be dynamically added or deleted without affecting the other pieces. - Dynamic: Security can be easily enhanced without changing the secret, but by changing the polynomial occasionally (keeping the same free term) and constructing new shares to the participants.
- Flexible: In organizations where hierarchy is important, we can supply each participant different number of pieces according to his importance inside the organization. For instance, the president can unlock the safe alone, whereas 3 secretaries are required together to unlock it.
See also
- Secret sharingSecret sharingSecret sharing refers to method for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together; individual shares are of no use on their own.More formally, in a...
- Lagrange polynomialLagrange polynomialIn numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
- Homomorphic secret sharingHomomorphic secret sharingIn cryptography, homomorphic secret sharing is a type of secret sharing algorithm in which the secret is encrypted via homomorphic encryption. A homomorphism is a transformation from one type of algebraic structure into another so that the structure is preserved...
- A simplistic decentralized voting protocol.
External links
- ssss: A free (GPL) implementation of Shamir's Scheme with online demo
- A perl implementation of Shamir's Secret Sharing
- Secret Sharp: A free (GPL) implementation of Shamir's Scheme for windows
- Christophe David's web based implementation of Shamir's scheme 'How to share a Secret'
- Shamir's Secret Sharing in Java : A free (LGPL) implementation of Shamir's scheme in Java

