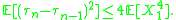Skorokhod's embedding theorem
Encyclopedia
In mathematics
and probability theory
, Skorokhod's embedding theorem is either or both of two theorem
s that allow one to regard any suitable collection of random variable
s as a Wiener process
(Brownian motion
) evaluated at a collection of stopping times. Both results are named for the Ukrainian
mathematician
A.V. Skorokhod
.
-valued random variable with expected value
0 and finite variance
; let W denote a canonical real-valued Wiener process. Then there is a stopping time (with respect to the natural filtration
of W), τ, such that Wτ has the same distribution as X,
and
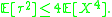
, each with expected value 0 and finite variance, and let
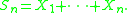
Then there is a non-decreasing (a.k.a. weakly increasing) sequence τ1, τ2, ... of stopping times such that the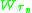
have the same joint distributions as the partial sums Sn and τ1, τ2 − τ1, τ3 − τ2, ... are independent and identically distributed random variables satisfying
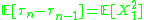
and
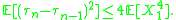
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Skorokhod's embedding theorem is either or both of two theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s that allow one to regard any suitable collection of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s as a Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
(Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
) evaluated at a collection of stopping times. Both results are named for the Ukrainian
Ukraine
Ukraine is a country in Eastern Europe. It has an area of 603,628 km², making it the second largest contiguous country on the European continent, after Russia...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
A.V. Skorokhod
Anatoliy Skorokhod
Anatoliy Volodymyrovych Skorokhod was a Soviet and Ukrainian mathematician, and an academician of the National Academy of Sciences of Ukraine from 1985 to his death in 2011....
.
Skorokhod's first embedding theorem
Let X be a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued random variable with expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
0 and finite variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
; let W denote a canonical real-valued Wiener process. Then there is a stopping time (with respect to the natural filtration
Filtration (abstract algebra)
In mathematics, a filtration is an indexed set Si of subobjects of a given algebraic structure S, with the index i running over some index set I that is a totally ordered set, subject to the condition that if i ≤ j in I then Si ⊆ Sj...
of W), τ, such that Wτ has the same distribution as X,
and
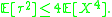
Skorokhod's second embedding theorem
Let X1, X2, ... be a sequence of independent and identically distributed random variablesIndependent and identically distributed random variables
In probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
, each with expected value 0 and finite variance, and let
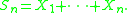
Then there is a non-decreasing (a.k.a. weakly increasing) sequence τ1, τ2, ... of stopping times such that the
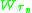have the same joint distributions as the partial sums Sn and τ1, τ2 − τ1, τ3 − τ2, ... are independent and identically distributed random variables satisfying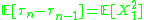and