Slepian's lemma
Encyclopedia
In probability theory
, Slepian's lemma (1962), named after David Slepian
, is a Gaussian comparison inequality. It states that for Gaussian random variables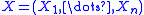
and 
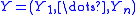in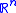 
satisfying 
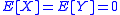and
for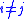 
,
the following inequality holds for all real numbers
:
,
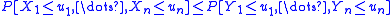While this intuitive-seeming result is true for Gaussian processes, it is not in general true for other random variables—not even those with expectation 0.
As a corollary, if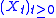
is a centered stationary
Gaussian process such that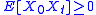
for all t, it holds for any real number c that
.
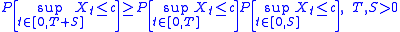, extreme value theory
and areas of pure probability. It has also been reproven in several different forms.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Slepian's lemma (1962), named after David Slepian
David Slepian
David S. Slepian was an American mathematician.Born in Pittsburgh, Pennsylvania he studied B.Sc. at University of Michigan before joining the forces in World War II,as Sonic deception officer in the Ghost army....
, is a Gaussian comparison inequality. It states that for Gaussian random variables
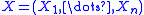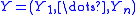and in 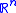satisfying 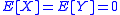and for 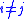,the following inequality holds for all real numbers
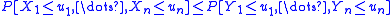:,While this intuitive-seeming result is true for Gaussian processes, it is not in general true for other random variables—not even those with expectation 0.
As a corollary, if
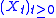is a centered stationaryStationary
Stationary can mean:* In statistics and probability: a stationary process.* In mathematics: a stationary point.* In mathematics: a stationary set.* In physics: a time-invariant quantity, such as a constant position or temperature....
Gaussian process such that
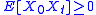for all t, it holds for any real number c that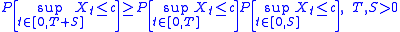.History
Slepian's lemma was first proven by Slepian in 1962, and has since been used in reliability theoryReliability theory
Reliability theory describes the probability of a system completing its expected function during an interval of time. It is the basis of reliability engineering, which is an area of study focused on optimizing the reliability, or probability of successful functioning, of systems, such as airplanes,...
, extreme value theory
Extreme value theory
Extreme value theory is a branch of statistics dealing with the extreme deviations from the median of probability distributions. The general theory sets out to assess the type of probability distributions generated by processes...
and areas of pure probability. It has also been reproven in several different forms.