
Specht's theorem
Encyclopedia
In mathematics, Specht's theorem gives a necessary and sufficient condition for two matrices
to be unitarily equivalent. It is named after Wilhelm Specht
, who proved the theorem in 1940.
Two matrices A and B are said to be unitarily equivalent if there exists a unitary matrix U such that B = U *AU. Two matrices which are unitarily equivalent are also similar. Two similar matrices represent the same linear map, but with respect to a different basis; unitary equivalence corresponds to a change from an orthonormal basis
to another orthonormal basis.
If A and B are unitarily equivalent, then tr AA* = tr BB*, where tr denotes the trace
(in other words, the Frobenius norm is a unitary invariant). This follows from the cyclic invariance of the trace: if B = U *AU, then tr BB* = tr U *AUU *A*U = tr AUU *A*UU * = tr AA*, where the second equality is cyclic invariance.
Thus, tr AA* = tr BB* is a necessary condition for unitary equivalence, but it is not sufficient. Specht's theorem gives infinitely many necessary conditions which together are also sufficient. The formulation of the theorem uses the following definition. A word in two variables, say x and y, is an expression of the form

where m1, n1, m2, n2, …, mp are non-negative integers. The degree of this word is

Specht's theorem: Two matrices A and B are unitarily equivalent if and only if tr W(A, A*) = tr W(B, B*) for all words W.
The theorem gives an infinite number of trace identities, but it can be reduced to a finite subset. Let n denote the size of the matrices A and B. For the case n = 2, the following three conditions are sufficient:
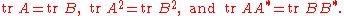
For n = 3, the following seven conditions are sufficient:
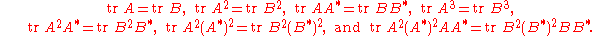
For general n, it suffices to show that tr W(A, A*) = tr W(B, B*) for all words of degree at most

It has been conjectured that this can be reduced to an expression linear in n.
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
to be unitarily equivalent. It is named after Wilhelm Specht
Wilhelm Specht
Wilhelm Otto Ludwig Specht was a mathematician who introduced Specht modules. He also proved the Specht criterion for unitary equivalence of matrices....
, who proved the theorem in 1940.
Two matrices A and B are said to be unitarily equivalent if there exists a unitary matrix U such that B = U *AU. Two matrices which are unitarily equivalent are also similar. Two similar matrices represent the same linear map, but with respect to a different basis; unitary equivalence corresponds to a change from an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
to another orthonormal basis.
If A and B are unitarily equivalent, then tr AA* = tr BB*, where tr denotes the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
(in other words, the Frobenius norm is a unitary invariant). This follows from the cyclic invariance of the trace: if B = U *AU, then tr BB* = tr U *AUU *A*U = tr AUU *A*UU * = tr AA*, where the second equality is cyclic invariance.
Thus, tr AA* = tr BB* is a necessary condition for unitary equivalence, but it is not sufficient. Specht's theorem gives infinitely many necessary conditions which together are also sufficient. The formulation of the theorem uses the following definition. A word in two variables, say x and y, is an expression of the form

where m1, n1, m2, n2, …, mp are non-negative integers. The degree of this word is

Specht's theorem: Two matrices A and B are unitarily equivalent if and only if tr W(A, A*) = tr W(B, B*) for all words W.
The theorem gives an infinite number of trace identities, but it can be reduced to a finite subset. Let n denote the size of the matrices A and B. For the case n = 2, the following three conditions are sufficient:
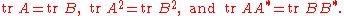
For n = 3, the following seven conditions are sufficient:
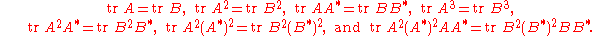
For general n, it suffices to show that tr W(A, A*) = tr W(B, B*) for all words of degree at most

It has been conjectured that this can be reduced to an expression linear in n.

