
Spouge's approximation
Encyclopedia
In mathematics
, Spouge's approximation is a formula for the gamma function
due to John L. Spouge. The formula is a modification of Stirling's approximation
, and has the form
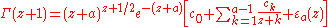
where a is an arbitrary positive integer and the coefficients are given by
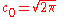
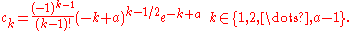
Spouge has proved that, if Re(z) > 0 and a > 2, the relative error in discarding εa(z) is bounded by
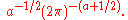
The formula is similar to the Lanczos approximation, but has some distinct features. Whereas the Lanczos formula exhibits faster convergence, Spouge's coefficients are much easier to calculate and the error can be set arbitrarily low. The formula is therefore feasible for arbitrary-precision
evaluation of the gamma function. However, special care must be taken to use sufficient precision when computing the sum due to the large size of the coefficients c_k, as well as their alternating sign. For example, for a=49, you must compute the sum using about 65 decimal digits of precision in order to obtain the promised 40 decimal digits of accuracy.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Spouge's approximation is a formula for the gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
due to John L. Spouge. The formula is a modification of Stirling's approximation
Stirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
, and has the form
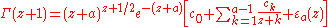
where a is an arbitrary positive integer and the coefficients are given by
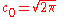
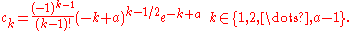
Spouge has proved that, if Re(z) > 0 and a > 2, the relative error in discarding εa(z) is bounded by
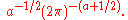
The formula is similar to the Lanczos approximation, but has some distinct features. Whereas the Lanczos formula exhibits faster convergence, Spouge's coefficients are much easier to calculate and the error can be set arbitrarily low. The formula is therefore feasible for arbitrary-precision
Arbitrary-precision arithmetic
In computer science, arbitrary-precision arithmetic indicates that calculations are performed on numbers whose digits of precision are limited only by the available memory of the host system. This contrasts with the faster fixed-precision arithmetic found in most ALU hardware, which typically...
evaluation of the gamma function. However, special care must be taken to use sufficient precision when computing the sum due to the large size of the coefficients c_k, as well as their alternating sign. For example, for a=49, you must compute the sum using about 65 decimal digits of precision in order to obtain the promised 40 decimal digits of accuracy.
External links
- Gamma function with Spouge's formula - MathematicaMathematicaMathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
implementation at LiteratePrograms

