In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, Stewart's theorem yields a relation between a lengths of the sides of the triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

 and the length of a cevian

Cevian

In geometry, a cevian is any line segment in a triangle with one endpoint on a vertex of the triangle and the other endpoint on the opposite side. Medians, altitudes, and angle bisectors are special cases of cevians...

 of the triangle. Its name is in honor of the Scottish mathematician Matthew Stewart who published the theorem in 1746.

Theorem

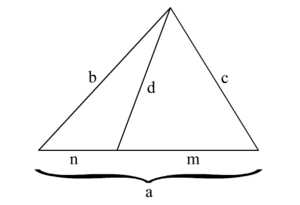
Let , , 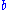and be the lengths of the sides of a triangle. Let 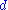be the length of a cevian to the side of length . If the cevian divides into two segments of length and , then Stewart's theorem states that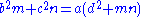
Apollonius' theorem

Apollonius' theorem

In geometry, Apollonius' theorem is a theorem relating the length of a median of a triangle to the lengths of its side.Specifically, in any triangle ABC, if AD is a median, thenAB^2 + AC^2 = 2\,...

 is the special case where d is the length of the Median

Median (geometry)

In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposing side. Every triangle has exactly three medians; one running from each vertex to the opposite side...

.

The theorem may be written somewhat more symmetrically using signed lengths of segments, in other words the length AB is taken to be positive or negative according to whether A is to the left or right of B in some fixed orientation of the line. In this formulation, the theorem states that if A, B, and C are collinear points, and P is any point, then

Proof

The theorem can be proved as an application of the law of cosines

Law of cosines

In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...

:

Let θ be the angle between m and d and θ′ the angle between n and d. Then θ′ is the supplement of θ and cos θ′ = −cos θ. The law of cosines for θ and θ′ states

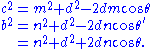
Multiply the first equation by n, the second equation by m, and add to eliminate cos θ, obtaining
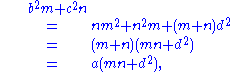
which is equation required.

Alternatively, the theorem can proved by drawing a perpendicular from the vertex of the triangle to the base and using the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

to write the distances b, c, and d in terms of the altitude. The left and right hand sides of the equation then reduce algebraically to the same expression.