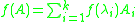Sylvester's formula
Encyclopedia
In matrix theory, Sylvester's formula or Sylvester's matrix theorem (named after J. J. Sylvester
) expresses an analytic function
f(A) of a matrix
A in terms of the eigenvalues and eigenvectors
of A. It states that
where the λi are the eigenvalues of A, and the matrices Ai are the corresponding Frobenius covariant
s of A.
Sylvester's formula is only valid for diagonalizable matrices
; an extension due to Buchheim covers the general case.
A with k distinct eigenvalues, λ1, …, λk, and any function f defined on some subset of the complex numbers such that f(A) is well defined. The last condition means that every eigenvalue λi is in the domain of f, and that every eigenvalue λi with multiplicity mi > 1 is in the interior of the domain, with f being (mi − 1) times differentiable at λi..
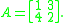
This matrix has two eigenvalues, 5 and −2. Its Frobenius covariants are

Sylvester's formula then states that
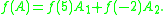
For instance, if f is defined by f(x) = x−1, then Sylvester's formula computes the matrix inverse f(A) = A−1 as
James Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
) expresses an analytic function
Matrix function
In mathematics, a matrix function is a function which maps a matrix to another matrix.- Extending scalar functions to matrix functions :There are several techniques for lifting a real function to a square matrix function such that interesting properties are maintained...
f(A) of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A in terms of the eigenvalues and eigenvectors
Eigenvalue, eigenvector and eigenspace
The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
of A. It states that
where the λi are the eigenvalues of A, and the matrices Ai are the corresponding Frobenius covariant
Frobenius covariant
In matrix theory, the Frobenius covariants of a square matrix A are matrices Ai associated with the eigenvalues and eigenvectors of A...
s of A.
Sylvester's formula is only valid for diagonalizable matrices
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
; an extension due to Buchheim covers the general case.
Conditions
Sylvester's formula applies for any diagonalizable matrixDiagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
A with k distinct eigenvalues, λ1, …, λk, and any function f defined on some subset of the complex numbers such that f(A) is well defined. The last condition means that every eigenvalue λi is in the domain of f, and that every eigenvalue λi with multiplicity mi > 1 is in the interior of the domain, with f being (mi − 1) times differentiable at λi..
Example
Consider the two-by-two matrix: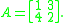
This matrix has two eigenvalues, 5 and −2. Its Frobenius covariants are

Sylvester's formula then states that
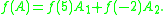
For instance, if f is defined by f(x) = x−1, then Sylvester's formula computes the matrix inverse f(A) = A−1 as