
Tarski's exponential function problem
Encyclopedia
In model theory
, Tarski
's exponential function problem asks whether the usual theory of the real number
s together with the exponential function
is decidable
. Tarski had previously shown that the theory of the real numbers (without the exponential function) is decidable.
s Lor = (+,·,−,<,0,1), with the usual interpretation given to each symbol. It was proved by Tarski that the theory of the real field
, Th(R), is decidable. That is, given any Lor-sentence φ there is an effective procedure for determining whether
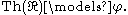
He then asked whether this was still the case if one added a unary function exp to the language that was interpreted as the exponential function
on R, to get the structure Rexp.
in n variables and with coefficients in Z has a solution in Rn. showed that Schanuel's conjecture
implies such a procedure exists, and hence gave a conditional solution to Tarski's problem. Schanuel's conjecture deals with all complex numbers so would be expected to be a stronger result than the decidability of Rexp, and indeed, Macintyre and Wilkie proved that only a real version of Schanuel's conjecture is required to imply the decidability of this theory.
Even the real version of Schanuel's conjecture is not a necessary condition for the decidability of the theory. In their paper, Macintyre and Wilkie showed that an equivalent result to the decidability of Th(Rexp) is what they dubbed the Weak Schanuel's Conjecture. This conjecture states that there is an effective procedure that, given n ≥ 1 and exponential polynomials in n variables with integer coefficients f1,..., fn, g, produces an integer η ≥ 1 that depends on n, f1,..., fn, g, and such that if α ∈ Rn is a non-singular
solution of the system
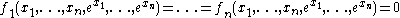
then either g(α) = 0 or |g(α)| > η−1.
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, Tarski
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
's exponential function problem asks whether the usual theory of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s together with the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
is decidable
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
. Tarski had previously shown that the theory of the real numbers (without the exponential function) is decidable.
The problem
The ordered real field R is a structure over the language of ordered ringOrdered ring
In abstract algebra, an ordered ring is a commutative ring R with a total order ≤ such that for all a, b, and c in R:* if a ≤ b then a + c ≤ b + c.* if 0 ≤ a and 0 ≤ b then 0 ≤ ab....
s Lor = (+,·,−,<,0,1), with the usual interpretation given to each symbol. It was proved by Tarski that the theory of the real field
Real closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
, Th(R), is decidable. That is, given any Lor-sentence φ there is an effective procedure for determining whether
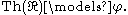
He then asked whether this was still the case if one added a unary function exp to the language that was interpreted as the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
on R, to get the structure Rexp.
Conditional and equivalent results
The problem can be reduced to finding an effective procedure for determining whether any given exponential polynomialExponential polynomial
In mathematics, exponential polynomials are functions on fields, rings, or abelian groups that take the form of polynomials in a variable and an exponential function.-In fields:...
in n variables and with coefficients in Z has a solution in Rn. showed that Schanuel's conjecture
Schanuel's conjecture
In mathematics, specifically transcendence theory, Schanuel's conjecture is a conjecture made by Stephen Schanuel in the 1960s concerning the transcendence degree of certain field extensions of the rational numbers.-Statement:The conjecture is as follows:...
implies such a procedure exists, and hence gave a conditional solution to Tarski's problem. Schanuel's conjecture deals with all complex numbers so would be expected to be a stronger result than the decidability of Rexp, and indeed, Macintyre and Wilkie proved that only a real version of Schanuel's conjecture is required to imply the decidability of this theory.
Even the real version of Schanuel's conjecture is not a necessary condition for the decidability of the theory. In their paper, Macintyre and Wilkie showed that an equivalent result to the decidability of Th(Rexp) is what they dubbed the Weak Schanuel's Conjecture. This conjecture states that there is an effective procedure that, given n ≥ 1 and exponential polynomials in n variables with integer coefficients f1,..., fn, g, produces an integer η ≥ 1 that depends on n, f1,..., fn, g, and such that if α ∈ Rn is a non-singular
Singular point of a curve
In geometry, a singular point on a curve is one where the curve is not given by a smooth embedding of a parameter. The precise definition of a singular point depends on the type of curve being studied.-Algebraic curves in the plane:...
solution of the system
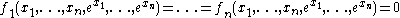
then either g(α) = 0 or |g(α)| > η−1.

