Tennenbaum's theorem
Encyclopedia
Tennenbaum's theorem, named for Stanley Tennenbaum
who presented the theorem in 1959, is a result in mathematical logic
that states that no countable
nonstandard model of Peano arithmetic
(PA) can be recursive
.
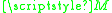in the language of PA is recursive if there are recursive functions + and × from 
to 
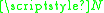, a recursive two-place relation < on 
, and distinguished constants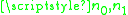 
such that
Stanley Tennenbaum
Stanley Tennenbaum was an American mathematician who contributed to the field of logic. In 1959, he published Tennenbaum's theorem, which states that no countable nonstandard model of Peano arithmetic can be recursive....
who presented the theorem in 1959, is a result in mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
that states that no countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
nonstandard model of Peano arithmetic
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
(PA) can be recursive
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
.
Recursive structures for PA
A structureModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
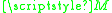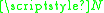in the language of PA is recursive if there are recursive functions + and × from to , a recursive two-place relation < on , and distinguished constants 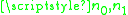such that-
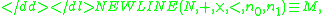
where
indicates isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
and
is the set of (standard) natural numbers. Because the isomorphism must be a bijection, every recursive model is countable. There are many nonisomorphic countable nonstandard models of PA.
Statement of the theorem
Tennenbaum's theorem states that no countable nonstandard model of PA is recursive. Moreover, neither the addition nor the multiplication of such a model can be recursive.
External links
- "Tennenbaum's Theorem for Models of Arithmetic" by R. W. Kaye http://web.mat.bham.ac.uk/R.W.Kaye/papers/tennenbaum/tennenbaum.pdf