In number theory, Tijdeman's theorem states that there are at most a finite number of consecutive powers. Stated another way, the set of solutions in integers x, y, n, m of the exponential diophantine equation


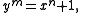
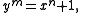
for exponents n and m greater than one, is finite.

The theorem was proven by Dutch number theorist Robert Tijdeman

Robert Tijdeman

Robert Tijdeman is a Dutch mathematician. Specializing in number theory, he is best known for his Tijdeman's theorem. He is a professor of mathematics at the Leiden University since 1975, and was chairman of the department of mathematics and computer science at Leiden from 1991 to 1993...

 in 1976, and provided a strong impetus towards the eventual proof of Catalan's conjecture by Preda Mihăilescu

Preda Mihailescu

Preda V. Mihăilescu is a Romanian mathematician, best known for his proof of Catalan's conjecture.Born in Bucharest, he is the brother of Vintilă Mihăilescu. After leaving Romania in 1973, he settled in Switzerland. He studied mathematics and computer science in Zürich, receiving his Ph.D. from...

. Mihăilescu's theorem

Mihailescu's theorem

Catalan's conjecture is a theorem in number theory that was conjectured by the mathematician Eugène Charles Catalan in 1844 and proven in 2002 by Preda Mihăilescu....

 states that there is only one member to the set of consecutive power pairs, namely 9=8+1.

That the powers are consecutive is essential to Tijdeman's proof; if we replace a difference of one by any other difference k and ask for the number of solutions
of


with n and m greater than one we have an unsolved problem. It is conjectured that this set also will be finite; its finiteness would follow, for instance, from the abc conjecture

Abc conjecture

The abc conjecture is a conjecture in number theory, first proposed by Joseph Oesterlé and David Masser in 1985. The conjecture is stated in terms of three positive integers, a, b and c , which have no common factor and satisfy a + b = c...

.