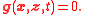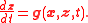Tikhonov's theorem (dynamical systems)
Encyclopedia
In applied mathematics, Tikhonov's theorem on dynamical systems is a result on stability of solutions of systems of differential equation
s. It has applications to chemical kinetics
. The theorem is named after Andrey Nikolayevich Tikhonov.
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s. It has applications to chemical kinetics
Chemical kinetics
Chemical kinetics, also known as reaction kinetics, is the study of rates of chemical processes. Chemical kinetics includes investigations of how different experimental conditions can influence the speed of a chemical reaction and yield information about the reaction's mechanism and transition...
. The theorem is named after Andrey Nikolayevich Tikhonov.
Statement
Consider this system of differential equations:-
Taking the limit as
, this becomes the "degenerate system":
-
where the second equation is the solution of the algebraic equation
Note that there may be more than one such function φ.
Tikhonov's theorem states that as
the solution of the system of two differential equations above approaches the solution of the degenerate system if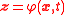 
is a stable root of the "adjoined system"
External links
-
-
