Trudinger's theorem
Encyclopedia
In mathematical analysis
, Trudinger's theorem or the Trudinger inequality (also sometimes called the Moser–Trudinger inequality) is a result of functional analysis
on Sobolev space
s. It is named after Neil Trudinger
(and Jürgen Moser
).
It provides an inequality between a certain Sobolev space
norm and an Orlicz space norm of a function. The inequality is a limiting case of Sobolev imbedding and can be stated as the following theorem:
Let
be a bounded domain in 
satisfying the cone condition. Let 
and 
. Set
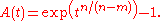
Then there exists the imbedding
where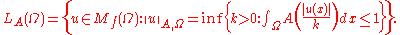
The space
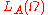
is an example of an Orlicz space.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, Trudinger's theorem or the Trudinger inequality (also sometimes called the Moser–Trudinger inequality) is a result of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
on Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s. It is named after Neil Trudinger
Neil Trudinger
Neil Sidney Trudinger is an Australian mathematician, known particularly for his work in the field of nonlinear elliptic partial differential equations....
(and Jürgen Moser
Jürgen Moser
Jürgen Kurt Moser or Juergen Kurt Moser was a German-American mathematician.-Professional biography:...
).
It provides an inequality between a certain Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
norm and an Orlicz space norm of a function. The inequality is a limiting case of Sobolev imbedding and can be stated as the following theorem:
Let
be a bounded domain in satisfying the cone condition. Let and . Set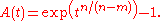Then there exists the imbedding
where
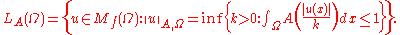
The space
is an example of an Orlicz space.