
Tucker's lemma
Encyclopedia
In mathematics, Tucker's lemma is a combinatorial
analog of the Borsuk–Ulam theorem.
Let T be a triangulation of the closed n-dimensional ball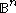 . Assume T is antipodally symmetric on the boundary
. Assume T is antipodally symmetric on the boundary 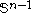 . That means that the subset of simplices of T which are in
. That means that the subset of simplices of T which are in  provides a triangulation of
provides a triangulation of  where if σ is a simplex then so is −σ. Let
where if σ is a simplex then so is −σ. Let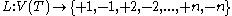
be a labelling of the vertices of T which satisfies L(−v)=−L(v) for all vertices v in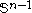 . Then Tucker's Lemma states that there exists a 1-simplex in T whose vertices are labelled by the same number but with opposite signs.
. Then Tucker's Lemma states that there exists a 1-simplex in T whose vertices are labelled by the same number but with opposite signs.
In the above example, where n=2, the red 1-simplex has vertices which are labelled by the same number with opposite signs. Tucker's lemma states that for such a triangulation at least one such 1-simplex must exist.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
analog of the Borsuk–Ulam theorem.
Let T be a triangulation of the closed n-dimensional ball
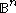 . Assume T is antipodally symmetric on the boundary
. Assume T is antipodally symmetric on the boundary 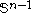 . That means that the subset of simplices of T which are in
. That means that the subset of simplices of T which are in  provides a triangulation of
provides a triangulation of  where if σ is a simplex then so is −σ. Let
where if σ is a simplex then so is −σ. Let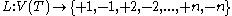
be a labelling of the vertices of T which satisfies L(−v)=−L(v) for all vertices v in
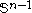 . Then Tucker's Lemma states that there exists a 1-simplex in T whose vertices are labelled by the same number but with opposite signs.
. Then Tucker's Lemma states that there exists a 1-simplex in T whose vertices are labelled by the same number but with opposite signs.In the above example, where n=2, the red 1-simplex has vertices which are labelled by the same number with opposite signs. Tucker's lemma states that for such a triangulation at least one such 1-simplex must exist.
See also
- Brouwer fixed point theoremBrouwer fixed point theoremBrouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
- Borsuk–Ulam theorem
- Topological combinatoricsTopological combinatoricsThe discipline of combinatorial topology used combinatorial concepts in topology and in the early 20th century this gradually turned into the field of algebraic topology....

