
Turán–Kubilius inequality
Encyclopedia
The Turán–Kubilius inequality is a mathematical theorem in probabilistic number theory
. It is useful for proving results about the normal order of an arithmetic function
. The theorem was proved in a special case in 1934 by Paul Turán and generalized in 1956 and 1964 by Jonas Kubilius
.
and in Cojocaru & Murty.
Suppose f is an additive
complex-valued arithmetic function
, and write p for an arbitrary prime and for an arbitrary positive integer. Write
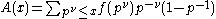
and
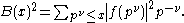
Then there is a function ε(x) that goes to zero when x goes to infinity, and such that for x ≥ 2 we have
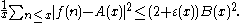
about the normal order
of the number ω(n) of distinct prime divisors of an integer n. There is an exposition of Turán's proof in Hardy & Wright, §22.11.
Tenenbaum gives a proof of the Hardy–Ramanujan theorem using the Turán–Kubilus inequality and states without proof several other applications.
Probabilistic number theory
Probabilistic number theory is a subfield of number theory, which explicitly uses probability to answer questions of number theory. One basic idea underlying it is that different prime numbers are, in some serious sense, like independent random variables...
. It is useful for proving results about the normal order of an arithmetic function
Normal order of an arithmetic function
In number theory, the normal order of an arithmetic function is some simpler or better-understood function which "usually" takes the same or closely approximate values.Let ƒ be a function on the natural numbers...
. The theorem was proved in a special case in 1934 by Paul Turán and generalized in 1956 and 1964 by Jonas Kubilius
Jonas Kubilius
Jonas Kubilius was a Lithuanian mathematician who worked in probability theory and number theory. He was rector of Vilnius University for 32 years, and served one term in the Lithuanian parliament.-Life and education:...
.
Statement of the theorem
This formulation is from Tenenbaum. Other formulations are in Narkiewiczand in Cojocaru & Murty.
Suppose f is an additive
Additive function
In mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
complex-valued arithmetic function
Arithmetic function
In number theory, an arithmetic function is a real or complex valued function ƒ defined on the set of natural numbers In number theory, an arithmetic (or arithmetical) function is a real or complex valued function ƒ(n) defined on the set of natural numbers In number theory, an arithmetic (or...
, and write p for an arbitrary prime and for an arbitrary positive integer. Write
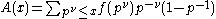
and
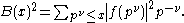
Then there is a function ε(x) that goes to zero when x goes to infinity, and such that for x ≥ 2 we have
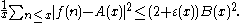
Applications of the theorem
Turán developed the inequality to create a simpler proof of the Hardy–Ramanujan theoremHardy–Ramanujan theorem
In mathematics, the Hardy–Ramanujan theorem, proved by , states that the normal order of the number ω of distinct prime factors of a number n is log...
about the normal order
Normal order of an arithmetic function
In number theory, the normal order of an arithmetic function is some simpler or better-understood function which "usually" takes the same or closely approximate values.Let ƒ be a function on the natural numbers...
of the number ω(n) of distinct prime divisors of an integer n. There is an exposition of Turán's proof in Hardy & Wright, §22.11.
Tenenbaum gives a proof of the Hardy–Ramanujan theorem using the Turán–Kubilus inequality and states without proof several other applications.

