
Ukkonen's algorithm
Encyclopedia
In 1995, Esko Ukkonen proposed a linear-time, online algorithm
for constructing suffix tree
s that has come to be known as Ukkonen's algorithm.
The algorithm begins with an implicit suffix tree containing the first character of the string. Then it steps through the string adding successive characters until the tree is complete. This order addition of characters gives Ukkonen's algorithm its "on-line" property; earlier algorithms proceeded backward from the last character. The naive implementation for generating a suffix tree requires O(n2)
or even O(n3)
time, where n is the length of the string. By exploiting a number of algorithmic techniques, Ukkonen reduced this to O(n) (linear) time, for constant-size alphabets, and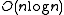 in general.
in general.
Online algorithm
In computer science, an online algorithm is one that can process its input piece-by-piece in a serial fashion, i.e., in the order that the input is fed to the algorithm, without having the entire input available from the start. In contrast, an offline algorithm is given the whole problem data from...
for constructing suffix tree
Suffix tree
In computer science, a suffix tree is a data structure that presents the suffixes of a given string in a way that allows for a particularly fast implementation of many important string operations.The suffix tree for a string S is a tree whose edges are labeled with strings, such that each suffix...
s that has come to be known as Ukkonen's algorithm.
The algorithm begins with an implicit suffix tree containing the first character of the string. Then it steps through the string adding successive characters until the tree is complete. This order addition of characters gives Ukkonen's algorithm its "on-line" property; earlier algorithms proceeded backward from the last character. The naive implementation for generating a suffix tree requires O(n2)
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
or even O(n3)
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
time, where n is the length of the string. By exploiting a number of algorithmic techniques, Ukkonen reduced this to O(n) (linear) time, for constant-size alphabets, and
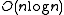 in general.
in general.External links
- Fast String Searching With Suffix Trees Mark Nelson's tutorial. Has an implementation example written with C++.
- Ukkonen's homepage

