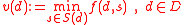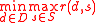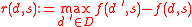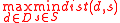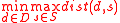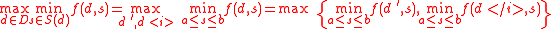Wald's maximin model
Encyclopedia
In decision theory
and game theory
, Wald's
maximin model is a non-probabilistic decision-making model according to which decisions are ranked on the basis of their worst-case outcomes. That is, the best (optimal) decision is one whose worst outcome is at least as good as the worst outcome of any other decisions. It is one of the most important models in robust decision making
in general and robust optimization
in particular.
It is also known by a variety of other titles, such as Wald's maximin rule, Wald's maximin principle, Wald's maximin paradigm, and Wald's maximin criterion. Often 'minimax
' is used instead of 'maximin'.
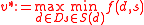
where denotes the decision space;
denotes the decision space; 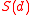 denotes the set of states associated with decision
denotes the set of states associated with decision  and
and  denotes the payoff (outcome) associated with decision
denotes the payoff (outcome) associated with decision  and state
and state  .
.
This model represents a 2-person game in which the player plays first. In response, the second player selects the worst state in
player plays first. In response, the second player selects the worst state in 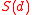 , namely a state in
, namely a state in 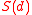 that minimizes the payoff
that minimizes the payoff 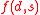 over
over  in
in 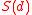 . In many applications the second player represents uncertainty. However, there are maximin models that are completely deterministic.
. In many applications the second player represents uncertainty. However, there are maximin models that are completely deterministic.
The above model is the classic format of Wald's maximin model. There is an equivalent mathematical programming
(MP) format:

where denotes the real line.
denotes the real line.
As in game theory
, the worst payoff associated with decision , namely
, namely
is called the security level of decision .
.
The minimax version of the model is obtained by exchanging the positions of the and
and  operations in the classic format:
operations in the classic format:
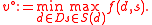
The equivalent MP format is as follows:
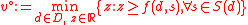
, Wald
developed this model in the early 1940s for situation where there is only one player (decision maker). The second player represents a pessimistic (worst case) approach to uncertainty. In Wald's maximin model, player 1 (the player) plays first and player 2 (the
player) plays first and player 2 (the  player) knows what decision was selected by player 1 when she selects her decision. This is a major simplification of the classic 2-person zero-sum game, in which the two players decide on their play without knowing the other player's choice. The game of Wald's maximin model is also a 2-person zero-sum game, but the players choose sequentially.
player) knows what decision was selected by player 1 when she selects her decision. This is a major simplification of the classic 2-person zero-sum game, in which the two players decide on their play without knowing the other player's choice. The game of Wald's maximin model is also a 2-person zero-sum game, but the players choose sequentially.
With the establishment of modern decision theory in the 1950s, the model became a key ingredient in the formulation of non-probabilistic decision-making models in the face of severe uncertainty. It is widely used in diverse fields such as decision theory
, control theory
, economics
, statistics
, robust optimization
, operations research
, philosophy, etc.
where denotes the real line. Formally we can set
denotes the real line. Formally we can set 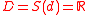 and
and  . The picture is this
. The picture is this
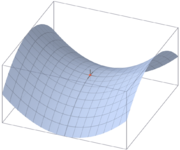
The optimal solution is the (red) saddle point
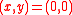 .
.
!
! Sun
! Rain
|-
! No umbrella
|5
|−9
|-
! Umbrella
|1
|−5
|}>
Appending a Worst Payoff column and a Best Worst Payoff column to the payoff table, we obtain
!
! Sun
! Rain
! Worst Payoff
! Best Worst Payoff
|-
! No umbrella
|5
|−9
|−9
|
|-
! Umbrella
|1
|−5
|−5
|−5
|}>
The worst case, if Henri goes out without umbrella, is definitely worse than the (best) worst case when carrying an umbrella. Therefore Henri takes his umbrella with him.
minimax regret model is an application of Wald's minimax model to the 'regrets' associated with the payoffs. It can be formulated as follows:
where
is the regret of payoff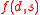 associated with the (decision,state) pair
associated with the (decision,state) pair 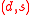 .
.
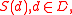 need not represent uncertainty. They can represent (deterministic) variations in the value of a parameter.
need not represent uncertainty. They can represent (deterministic) variations in the value of a parameter.
 be a finite set representing possible locations of an 'undesirable' public facility (e.g. garbage dump), and let
be a finite set representing possible locations of an 'undesirable' public facility (e.g. garbage dump), and let  denote a finite set of locations in the neighborhood of the planned facility, representing existing dwellings.
denote a finite set of locations in the neighborhood of the planned facility, representing existing dwellings.
It might be desirable to build the facility so that its shortest distance from an existing dwelling is as large as possible. The maximin formulation of the problem is as follows:
where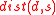 denotes the distance of
denotes the distance of  from
from  . Note that in this problem
. Note that in this problem 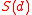 does not vary with
does not vary with  .
.
In cases where is it desirable to live close to the facility, the objective could be to minimize the maximum distance from the facility. This yields the following minimax problem:
These are generic facility location
problems.
The maximin formulation of this problem, in the MP format, is as follows:
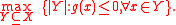
Generic problems of this type appear in robustness analysis.
It has been shown that the radius of stability
model and info-gap's robustness
model are simple instances of Wald's maximin model.
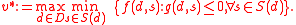
Its equivalent MP format is as follows:
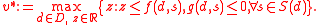
Such models are very useful in robust optimization
.
Now consider the instance shown by
Note that although the payoff associated with decision d' is larger than the payoff associated with decision d" over most of the state space S=[a,b], the best worst case according to Wald's model is provided by decision d". Hence, according to Wald's model decision d" is better than decision d'.
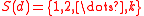 for all
for all  . The associated maximin problem is then as follows:
. The associated maximin problem is then as follows:
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
and game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, Wald's
Abraham Wald
- See also :* Sequential probability ratio test * Wald distribution* Wald–Wolfowitz runs test...
maximin model is a non-probabilistic decision-making model according to which decisions are ranked on the basis of their worst-case outcomes. That is, the best (optimal) decision is one whose worst outcome is at least as good as the worst outcome of any other decisions. It is one of the most important models in robust decision making
Robust decision making
Robust decision making is an iterative decision analytic framework that helps identify potential robust strategies, characterize the vulnerabilities of such strategies, and evaluate the tradeoffs among them...
in general and robust optimization
Robust optimization
Robust optimization is a field of optimization theory that deals with optimization problems where robustness is sought against uncertainty and/or variability in the value of a parameter of the problem.- History :...
in particular.
It is also known by a variety of other titles, such as Wald's maximin rule, Wald's maximin principle, Wald's maximin paradigm, and Wald's maximin criterion. Often 'minimax
Minimax
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
' is used instead of 'maximin'.
Definition
Wald's generic maximin model is as follows: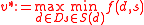
where
 denotes the decision space;
denotes the decision space; 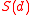 denotes the set of states associated with decision
denotes the set of states associated with decision  and
and  denotes the payoff (outcome) associated with decision
denotes the payoff (outcome) associated with decision  and state
and state  .
.This model represents a 2-person game in which the
 player plays first. In response, the second player selects the worst state in
player plays first. In response, the second player selects the worst state in 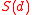 , namely a state in
, namely a state in 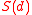 that minimizes the payoff
that minimizes the payoff 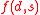 over
over  in
in 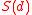 . In many applications the second player represents uncertainty. However, there are maximin models that are completely deterministic.
. In many applications the second player represents uncertainty. However, there are maximin models that are completely deterministic.The above model is the classic format of Wald's maximin model. There is an equivalent mathematical programming
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
(MP) format:

where
 denotes the real line.
denotes the real line.As in game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, the worst payoff associated with decision
 , namely
, namelyis called the security level of decision
 .
.The minimax version of the model is obtained by exchanging the positions of the
 and
and  operations in the classic format:
operations in the classic format: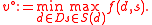
The equivalent MP format is as follows:
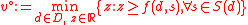
History
Inspired by maximin models of game theoryAbraham Wald
- See also :* Sequential probability ratio test * Wald distribution* Wald–Wolfowitz runs test...
, Wald
Wald
- Surname :* Kenneth Wald Sales Consultant U.S. Born* Abraham Wald , Hungarian mathematician of German descent* Carol Wald , American artist.* Charles F...
developed this model in the early 1940s for situation where there is only one player (decision maker). The second player represents a pessimistic (worst case) approach to uncertainty. In Wald's maximin model, player 1 (the
 player) plays first and player 2 (the
player) plays first and player 2 (the  player) knows what decision was selected by player 1 when she selects her decision. This is a major simplification of the classic 2-person zero-sum game, in which the two players decide on their play without knowing the other player's choice. The game of Wald's maximin model is also a 2-person zero-sum game, but the players choose sequentially.
player) knows what decision was selected by player 1 when she selects her decision. This is a major simplification of the classic 2-person zero-sum game, in which the two players decide on their play without knowing the other player's choice. The game of Wald's maximin model is also a 2-person zero-sum game, but the players choose sequentially.With the establishment of modern decision theory in the 1950s, the model became a key ingredient in the formulation of non-probabilistic decision-making models in the face of severe uncertainty. It is widely used in diverse fields such as decision theory
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
, control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, robust optimization
Robust optimization
Robust optimization is a field of optimization theory that deals with optimization problems where robustness is sought against uncertainty and/or variability in the value of a parameter of the problem.- History :...
, operations research
Operations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
, philosophy, etc.
Example
One of the most famous examples of a Maximin/Minimax model iswhere
 denotes the real line. Formally we can set
denotes the real line. Formally we can set 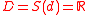 and
and  . The picture is this
. The picture is this
The optimal solution is the (red) saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
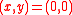 .
.Decision tables
There are many cases where it is convenient to 'organize' the Maximin/Minimax model as a 'table'. The convention is that the rows of the table represent the decisions, and the columns represent the states.Example
Henri is going for a walk. The sun may shine, or it may rain. Should Henri carry an umbrella? Henri does not like carrying an umbrella, but he dislikes getting wet even more. His "payoff matrix", viewing this as a Maximin game pitting Henri against Nature, is as follows.! Sun
! Rain
|-
! No umbrella
|
|
|-
! Umbrella
|
|
|}>
Appending a Worst Payoff column and a Best Worst Payoff column to the payoff table, we obtain
! Sun
! Rain
! Worst Payoff
! Best Worst Payoff
|-
! No umbrella
|
|
|
|
|-
! Umbrella
|
|
|
|
|}>
The worst case, if Henri goes out without umbrella, is definitely worse than the (best) worst case when carrying an umbrella. Therefore Henri takes his umbrella with him.
Variations on a theme
Over the years a variety of related models have been developed primarily to moderate the pessimistic approach dictated by the worst-case orientation of the model. For example,Savage's minimax regret
Savage'sLeonard Jimmie Savage
Leonard Jimmie Savage was an American mathematician and statistician. Nobel Prize-winning economist Milton Friedman said Savage was "one of the few people I have met whom I would unhesitatingly call a genius."...
minimax regret model is an application of Wald's minimax model to the 'regrets' associated with the payoffs. It can be formulated as follows:
where
is the regret of payoff
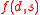 associated with the (decision,state) pair
associated with the (decision,state) pair 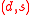 .
.Deterministic models
The sets of states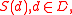 need not represent uncertainty. They can represent (deterministic) variations in the value of a parameter.
need not represent uncertainty. They can represent (deterministic) variations in the value of a parameter.Example
Let be a finite set representing possible locations of an 'undesirable' public facility (e.g. garbage dump), and let
be a finite set representing possible locations of an 'undesirable' public facility (e.g. garbage dump), and let  denote a finite set of locations in the neighborhood of the planned facility, representing existing dwellings.
denote a finite set of locations in the neighborhood of the planned facility, representing existing dwellings.It might be desirable to build the facility so that its shortest distance from an existing dwelling is as large as possible. The maximin formulation of the problem is as follows:
where
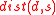 denotes the distance of
denotes the distance of  from
from  . Note that in this problem
. Note that in this problem 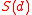 does not vary with
does not vary with  .
.In cases where is it desirable to live close to the facility, the objective could be to minimize the maximum distance from the facility. This yields the following minimax problem:
These are generic facility location
Facility location
Facility location, also known as location analysis, is a branch of operations research and computational geometry concerning itself with mathematical modeling and solution of problems concerning optimal placement of facilities in order to minimize transportation costs, avoid placing hazardous...
problems.
Maximin models in disguise
Experience has shown that the formulation of maximin models can be subtle in the sense that problems that 'do not look like' maximin problems can be formulated as such.Example
Consider the following problem:
Given a finite setand a real valued function
on
, find the largest subset of
such that
for every
in this subset.
The maximin formulation of this problem, in the MP format, is as follows:
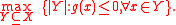
Generic problems of this type appear in robustness analysis.
It has been shown that the radius of stability
Stability radius
The stability radius of an object at a given nominal point is the radius of the largest ball, centered at the nominal point, all whose elements satisfy pre-determined stability conditions...
model and info-gap's robustness
Info-gap decision theory
Info-gap decision theory is a non-probabilistic decision theory that seeks to optimize robustness to failure – or opportuneness for windfall – under severe uncertainty, in particular applying sensitivity analysis of the stability radius type to perturbations in the value of a given estimate of the...
model are simple instances of Wald's maximin model.
Constrained maximin models
Constraints can be incorporated explicitly in the maximin models. For instance, the following is a constrained maximin problem stated in the classic format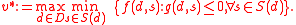
Its equivalent MP format is as follows:
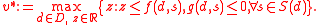
Such models are very useful in robust optimization
Robust optimization
Robust optimization is a field of optimization theory that deals with optimization problems where robustness is sought against uncertainty and/or variability in the value of a parameter of the problem.- History :...
.
The price of robustness
One of the 'weaknesses' of the Maximin model is that the robustness that it provides comes with a price. By playing it safe, the Maximin model tends to generate conservative decisions, whose price can be high. The following example illustrates this important feature of the model.Example
Consider the simple case where there are two decisions, d' and d", and where S(d')=S(d")=[a,b]. The Maximin model is then as follows:Now consider the instance shown by
Note that although the payoff associated with decision d' is larger than the payoff associated with decision d" over most of the state space S=[a,b], the best worst case according to Wald's model is provided by decision d". Hence, according to Wald's model decision d" is better than decision d'.
Algorithms
There are no general-purpose algorithms for the solution of maximin problems. Some problems are very simple to solve, others are very difficult.Example
Consider the case where the state variable is an "index", for instance let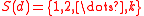 for all
for all  . The associated maximin problem is then as follows:
. The associated maximin problem is then as follows:-
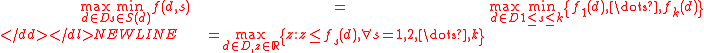
where .
.
If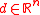 , all the functions
, all the functions 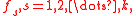 are linearLinearIn mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
are linearLinearIn mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
, and is specified by a system of linearLinearIn mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
is specified by a system of linearLinearIn mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
constraints on , then this problem is a linear programmingLinear programmingLinear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
, then this problem is a linear programmingLinear programmingLinear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problem that can be solved by linear programmingLinear programmingLinear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
algorithms such as the simplex algorithmSimplex algorithmIn mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
.