Watson's lemma
Encyclopedia
In mathematics, Watson's lemma, proved by G. N. Watson
(1918, p. 133), has significant application within the theory on the asymptotic behavior of integral
s.
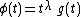, where 
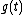has an infinite number of derivatives in the neighborhood of 
, with 
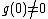, and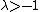 
.
Suppose, in addition, that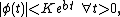
where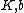
are independent of 
.
Then, it is true that for all positive
that
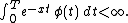
and the following asymptotic equivalence holds: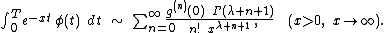
Proof: See, for instance, for the original proof or for a more recent development.
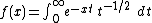
for large values of
, that is when 
.
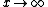Solution: By direct application of Watson's lemma, with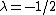
and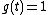 
,
so that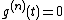
for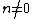 
. It is easy to see that:
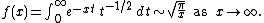
This development used the fact that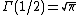
, a known property of the Gamma function
.
G. N. Watson
Neville Watson was an English mathematician, a noted master in the application of complex analysis to the theory of special functions. His collaboration on the 1915 second edition of E. T. Whittaker's A Course of Modern Analysis produced the classic “Whittaker & Watson” text...
(1918, p. 133), has significant application within the theory on the asymptotic behavior of integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s.
Statement of the lemma
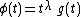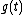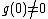Assume, where has an infinite number of derivatives in the neighborhood of , with , and 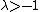.Suppose, in addition, that
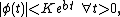
where
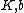are independent of .Then, it is true that for all positive
that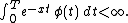and the following asymptotic equivalence holds:
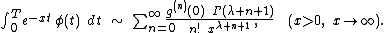
Proof: See, for instance, for the original proof or for a more recent development.
Example
Find a simple asymptotic approximation for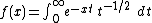for large values of
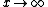, that is when .Solution: By direct application of Watson's lemma, with
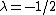and 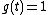,so that
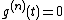for 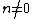. It is easy to see that: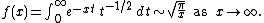This development used the fact that
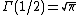, a known property of the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.