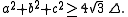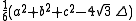Weitzenböck's inequality
Encyclopedia
In mathematics
, Weitzenböck's inequality (named after Roland Weitzenböck) states that for a triangle of side lengths ,
, 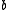 ,
,  , and area
, and area 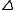 , the following inequality holds:
, the following inequality holds:
Equality occurs if and only if the triangle is equilateral. Pedoe's inequality
is a generalization of Weitzenböck's inequality.
of 1961. Even so, the result is not too difficult to derive using Heron's formula for the area of a triangle:
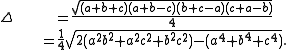
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Weitzenböck's inequality (named after Roland Weitzenböck) states that for a triangle of side lengths
 ,
, 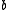 ,
,  , and area
, and area 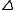 , the following inequality holds:
, the following inequality holds:Equality occurs if and only if the triangle is equilateral. Pedoe's inequality
Pedoe's inequality
In geometry, Pedoe's inequality, named after Daniel Pedoe, states that if a, b, and c are the lengths of the sides of a triangle with area ƒ, and A, B, and C are the lengths of the sides of a triangle with area F, then...
is a generalization of Weitzenböck's inequality.
Proofs
The proof of this inequality was set as a question in the International Mathematical OlympiadInternational Mathematical Olympiad
The International Mathematical Olympiad is an annual six-problem, 42-point mathematical olympiad for pre-collegiate students and is the oldest of the International Science Olympiads. The first IMO was held in Romania in 1959. It has since been held annually, except in 1980...
of 1961. Even so, the result is not too difficult to derive using Heron's formula for the area of a triangle:
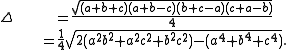
First method
This method assumes no knowledge of inequalities except that all squares are nonnegative.-
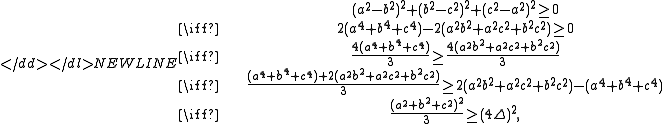
and the result follows immediately by taking the positive square root of both sides. From the first inequality we can also see that equality occurs only when and the triangle is equilateral.
and the triangle is equilateral.
Second method
This proof assumes knowledge of the rearrangement inequality and the arithmetic-geometric mean inequality.
-
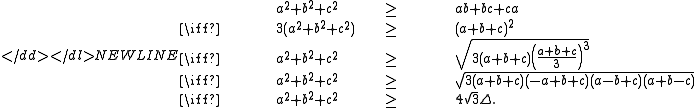
As we have used the rearrangement inequality and the arithmetic-geometric mean inequality, equality only occurs when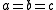 and the triangle is equilateral.
and the triangle is equilateral.
Third method
It can be shown that the area of the inner Napoleon's triangle is:
and therefore greater than or equal to 0.
External links
- "Weitzenböck's Inequality," an interactive demonstration by Jay Warendorff - Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
.
-
-