Wolfram's 2-state 3-symbol Turing machine
Encyclopedia
In his book A New Kind of Science
, Stephen Wolfram
described a universal 2-state 5-color Turing machine
, and conjectured that a particular 2-state 3-color Turing machine (hereinafter (2,3) Turing machine) might be universal
as well.
On May 14, 2007, Wolfram announced a $25,000 prize to be won by the first person to prove or disprove the universality of the (2,3) Turing machine. According to Wolfram, the purpose of the prize was to encourage research to help answer foundational questions associated with the structure of what he calls the "computational universe". On 24 October 2007, it was announced that the prize had been won by Alex Smith, a student in electronics and computing at the University of Birmingham
.
The (2,3) Turing machine:
Minsky (1967) briefly argues that standard (2,2) machines cannot be universal; thus, it might seem that the (2,3) Turing machine would be the smallest possible universal Turing machine
(in terms of number of states times number of symbols). However, the results are not directly comparable, because Minsky only considers machines which explicitly halt, which the (2, 3) machine does not. More generally, almost all formal definitions of Turing machines differ in details irrelevant to their power, but perhaps relevant to what can be expressed using a given number of states and symbols; there is no single standard formal definition. The (2,3) Turing machine also requires an infinite non-repeating input, again making a direct comparison to earlier small Turing machines problematic. Therefore, though it may be true that the (2, 3) machine is in some sense the "smallest possible universal Turing machine
", this has not been strictly proven, and the claim is open to debate.
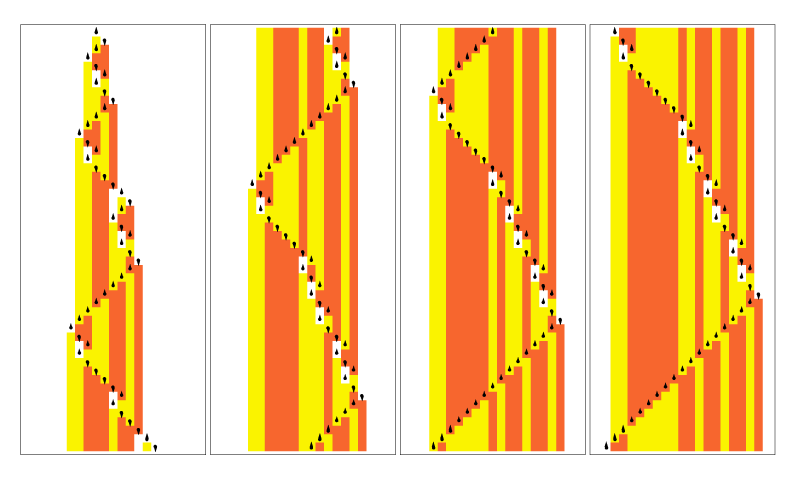
The state of the head (up or down droplet) and the pattern of colour (orange, yellow and white) in a given row depends solely on the content of the row immediately above it.
Even though the machine has a head with only two states, and a tape that can hold only three colours (depending on the initial content of the tape), the machine's output can still be remarkably complex.
(UK), proved that the (2,3) Turing machine is universal and thus won Wolfram's prize described above. Martin Davis
, a member of the committee, noted in a post to the FOM mailing list that:
The proof showed that the machine is equivalent to a variant of a tag system
already known to be universal. Smith first constructed a sequence of rule systems showing that the (2,3) Turing machine is capable of arbitrary finite computations. He then employed a novel approach to extend that construction to unbounded computations. The proof proceeds in two stages. The first part emulates the finite evolution of any two-color cyclic tag system. The emulation is a composite of a series of emulations involving the indexed rule systems 'system 0' through 'system 5'. Each rule system emulates the next one in the sequence. Smith then showed that even though the initial condition of the (2,3) Turing machine is not repetitive, the construction of that initial condition is not universal. Hence the (2,3) Turing machine is universal.
Vaughan Pratt disputed the correctness of this proof in a public list of discussion, noting that similar techniques would allow a linear bounded automaton
(or LBA) to be universal, which would contradict a known non-universality result due to Noam Chomsky
. Alex Smith joined the mailing list after this message and replied on the following day explaining that a LBA would require to be restarted manually to become universal using the same initial configuration, while his construction restarts the Turing machine automatically with no external intervention. Discussions about the proof continued for some time between Alex Smith, Vaughan Pratt, and others.
Wolfram claims that Smith's proof is another piece of evidence for Wolfram's general Principle of Computational Equivalence (PCE). That principle states that if one sees behavior that is not obviously simple, the behavior will correspond to a computation that is in a sense “maximally sophisticated”. Smith's proof has unleashed a debate on the precise operational conditions a Turing machine must satisfy in order for it to be candidate universal machine.
A universal (2,3) Turing machine has conceivable applications. For instance, a machine that small and simple can be embedded or constructed using a small number of particles or molecules. But the “compiler” Smith's algorithm implies does not produce compact or efficient code, at least for anything but the simplest cases. Hence the resulting code tends to be astronomically large and very inefficient. Whether there exist more efficient codings enabling the (2,3) Turing machine to compute more rapidly is an open question.
A New Kind of Science
A New Kind of Science is a book by Stephen Wolfram, published in 2002. It contains an empirical and systematic study of computational systems such as cellular automata...
, Stephen Wolfram
Stephen Wolfram
Stephen Wolfram is a British scientist and the chief designer of the Mathematica software application and the Wolfram Alpha computational knowledge engine.- Biography :...
described a universal 2-state 5-color Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
, and conjectured that a particular 2-state 3-color Turing machine (hereinafter (2,3) Turing machine) might be universal
Universal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
as well.
On May 14, 2007, Wolfram announced a $25,000 prize to be won by the first person to prove or disprove the universality of the (2,3) Turing machine. According to Wolfram, the purpose of the prize was to encourage research to help answer foundational questions associated with the structure of what he calls the "computational universe". On 24 October 2007, it was announced that the prize had been won by Alex Smith, a student in electronics and computing at the University of Birmingham
University of Birmingham
The University of Birmingham is a British Redbrick university located in the city of Birmingham, England. It received its royal charter in 1900 as a successor to Birmingham Medical School and Mason Science College . Birmingham was the first Redbrick university to gain a charter and thus...
.
Description
In each state, the machine reads the bit under the head and executes the instructions in the following table (where Pn prints bit n, L and R are left and right respectively, and A and B mean "switch to that state").| A | B | |
|---|---|---|
| 0 | P1,R,B | P2,L,A |
| 1 | P2,L,A | P2,R,B |
| 2 | P1,L,A | P0,R,A |
The (2,3) Turing machine:
- Has no halt state;
- Is trivially related to 23 other machines by interchange of states, colors and directions.
Minsky (1967) briefly argues that standard (2,2) machines cannot be universal; thus, it might seem that the (2,3) Turing machine would be the smallest possible universal Turing machine
Universal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
(in terms of number of states times number of symbols). However, the results are not directly comparable, because Minsky only considers machines which explicitly halt, which the (2, 3) machine does not. More generally, almost all formal definitions of Turing machines differ in details irrelevant to their power, but perhaps relevant to what can be expressed using a given number of states and symbols; there is no single standard formal definition. The (2,3) Turing machine also requires an infinite non-repeating input, again making a direct comparison to earlier small Turing machines problematic. Therefore, though it may be true that the (2, 3) machine is in some sense the "smallest possible universal Turing machine
Universal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
", this has not been strictly proven, and the claim is open to debate.

The state of the head (up or down droplet) and the pattern of colour (orange, yellow and white) in a given row depends solely on the content of the row immediately above it.
Even though the machine has a head with only two states, and a tape that can hold only three colours (depending on the initial content of the tape), the machine's output can still be remarkably complex.
Proof of universality
On 24 October 2007, it was announced by Wolfram Research (without the approval of the judging committee ) that Alex Smith, a student in electronics and computing at the University of BirminghamUniversity of Birmingham
The University of Birmingham is a British Redbrick university located in the city of Birmingham, England. It received its royal charter in 1900 as a successor to Birmingham Medical School and Mason Science College . Birmingham was the first Redbrick university to gain a charter and thus...
(UK), proved that the (2,3) Turing machine is universal and thus won Wolfram's prize described above. Martin Davis
Martin Davis
Martin David Davis, is an American mathematician, known for his work on Hilbert's tenth problem . He received his Ph.D. from Princeton University in 1950, where his adviser was Alonzo Church . He is Professor Emeritus at New York University. He is the co-inventor of the Davis-Putnam and the DPLL...
, a member of the committee, noted in a post to the FOM mailing list that:
- "As far as I know, no member of the committee has passed on the validity of this 40 page proof. The determination that Smith's proof is correct seems to have been made entirely by the Wolfram organization. My understanding is that the I/O involves complex encodings."
The proof showed that the machine is equivalent to a variant of a tag system
Tag system
A tag system is a deterministic computational model published by Emil Leon Post in 1943 as a simple form of Post canonical system. A tag system may also be viewed as an abstract machine, called a Post tag machine —briefly, a finite state machine whose only tape is a FIFO queue of unbounded length,...
already known to be universal. Smith first constructed a sequence of rule systems showing that the (2,3) Turing machine is capable of arbitrary finite computations. He then employed a novel approach to extend that construction to unbounded computations. The proof proceeds in two stages. The first part emulates the finite evolution of any two-color cyclic tag system. The emulation is a composite of a series of emulations involving the indexed rule systems 'system 0' through 'system 5'. Each rule system emulates the next one in the sequence. Smith then showed that even though the initial condition of the (2,3) Turing machine is not repetitive, the construction of that initial condition is not universal. Hence the (2,3) Turing machine is universal.
Vaughan Pratt disputed the correctness of this proof in a public list of discussion, noting that similar techniques would allow a linear bounded automaton
Linear bounded automaton
In computer science, a linear bounded automaton is a restricted form of nondeterministic Turing machine.-Operation:Linear bounded automata satisfy the following three conditions:...
(or LBA) to be universal, which would contradict a known non-universality result due to Noam Chomsky
Noam Chomsky
Avram Noam Chomsky is an American linguist, philosopher, cognitive scientist, and activist. He is an Institute Professor and Professor in the Department of Linguistics & Philosophy at MIT, where he has worked for over 50 years. Chomsky has been described as the "father of modern linguistics" and...
. Alex Smith joined the mailing list after this message and replied on the following day explaining that a LBA would require to be restarted manually to become universal using the same initial configuration, while his construction restarts the Turing machine automatically with no external intervention. Discussions about the proof continued for some time between Alex Smith, Vaughan Pratt, and others.
Wolfram claims that Smith's proof is another piece of evidence for Wolfram's general Principle of Computational Equivalence (PCE). That principle states that if one sees behavior that is not obviously simple, the behavior will correspond to a computation that is in a sense “maximally sophisticated”. Smith's proof has unleashed a debate on the precise operational conditions a Turing machine must satisfy in order for it to be candidate universal machine.
A universal (2,3) Turing machine has conceivable applications. For instance, a machine that small and simple can be embedded or constructed using a small number of particles or molecules. But the “compiler” Smith's algorithm implies does not produce compact or efficient code, at least for anything but the simplest cases. Hence the resulting code tends to be astronomically large and very inefficient. Whether there exist more efficient codings enabling the (2,3) Turing machine to compute more rapidly is an open question.
See also
- Turing machineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
- Universal Turing machineUniversal Turing machineIn computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
- Turing completenessTuring completenessIn computability theory, a system of data-manipulation rules is said to be Turing complete or computationally universal if and only if it can be used to simulate any single-taped Turing machine and thus in principle any computer. A classic example is the lambda calculus...
- Rule 110
- tag systemTag systemA tag system is a deterministic computational model published by Emil Leon Post in 1943 as a simple form of Post canonical system. A tag system may also be viewed as an abstract machine, called a Post tag machine —briefly, a finite state machine whose only tape is a FIFO queue of unbounded length,...
- automata theoryAutomata theoryIn theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...
- finite state machineFinite state machineA finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
Historical reading
- Marvin MinskyMarvin MinskyMarvin Lee Minsky is an American cognitive scientist in the field of artificial intelligence , co-founder of Massachusetts Institute of Technology's AI laboratory, and author of several texts on AI and philosophy.-Biography:...
(1967) Computation: Finite and Infinite Machines. Prentice Hall. - Turing, AAlan TuringAlan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
(1937) "On Computable Numbers with an Application to the Entscheidungsproblem," Proceedings of the London Mathematical Society Series 2, 42: 230-265. - ------ (1938) "On Computable Numbers, with an Application to the Entscheidungsproblem. A Correction," Proceedings of the London Mathematical Society Series 2, 43: 544-546.
External links
- "Student snags maths prize" Nature. Published online 24 October 2007.
- "College Kid Proves That Wolfram's Turing Machine is the Simplest Universal Computer," Wired Science. Published online 24 October 2007.
- "Simplest 'universal computer' wins student $25,000," New Scientist. Published online 24 October 2007.
- "The Wolfram Prize and Universal Computation: It's Your Problem Now," Dr. Dobbs Journal. Published online 22 October 2007.
- Minkel, J.R., "A New Kind of Science Author Pays Brainy Undergrad $25,000 for Identifying Simplest Computer," Scientific American, October 25, 2007.
- From Foundations of Mathematics discussion threads:

