Yao's Principle
Encyclopedia
In computational complexity theory
, Yao's principle or Yao's minimax principle states that the expected
cost of any randomized algorithm
for solving a given problem, on the worst case
input for that algorithm, can be no better than the expected cost, for a worst-case random probability distribution
on the inputs, of the deterministic algorithm
that performs best against that distribution. Thus, to establish a lower bound on the performance of randomized algorithms, it suffices to find an appropriate distribution of difficult inputs, and to prove that no deterministic algorithm can perform well against that distribution. This principle is named after Andrew Yao
, who first proposed it.
Yao's principle may be interpreted in game theoretic
terms, via a two-player zero sum game in which one player, Alice
, selects a deterministic algorithm, the other player, Bob, selects an input, and the payoff is the cost of the selected algorithm on the selected input. Any randomized algorithm R may be interpreted as a randomized choice among deterministic algorithms, and thus as a strategy for Alice. By von Neumann's
minimax theorem, Bob has a randomized strategy that performs at least as well against R as it does against the best pure strategy Alice might choose; that is, Bob's strategy defines a distribution on the inputs such that the expected cost of R on that distribution (and therefore also the worst case expected cost of R) is no better than the expected cost of any single deterministic algorithm against the same distribution.
randomized algorithms, i.e., distributions over deterministic algorithms that are correct on every input but have varying costs. It is straightforward to adapt the principle to Monte Carlo
algorithms, i.e., distributions over deterministic algorithms that have bounded costs but can be incorrect on some inputs.
Consider a problem over the inputs
, and let 
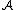be the set of all possible deterministic algorithms that correctly solve the problem.
For any algorithm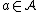
and input 
, let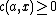 
be the cost of algorithm 
run on input 
.
Let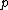
be a probability distributions over the algorithms 
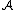, and let 
denote a random algorithm chosen according to 
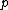. Let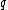 
be a probability distribution over the inputs 
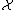, and let 
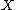denote a random input chosen according to 
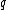. Then,
i.e., the worst-case expected cost of the randomized algorithm is at least the cost of the best deterministic algorithm against input distribution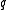
.
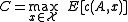. For every input 
, we have 
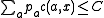. Therefore, 
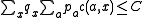. Using Fubini's theorem
, since all terms are non-negative we can switch the order of summation, giving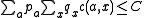
. By the Pigeonhole principle, there must exist an algorithm 
so that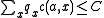 
, concluding the proof.
As mentioned above, this theorem can also be seen as a very special case of the Minimax theorem.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, Yao's principle or Yao's minimax principle states that the expected
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
cost of any randomized algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
for solving a given problem, on the worst case
Worst Case
Worst Case is the 3rd book in the Michael Bennett series from James Patterson and Michael Ledwidge.-Plot summary:NYPD Detective Mike Bennett and his new partner FBI Special Agent Emily Parker are on the trail of Francis Mooney, a Manhattan trusts and estates lawyer with terminal lung cancer...
input for that algorithm, can be no better than the expected cost, for a worst-case random probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
on the inputs, of the deterministic algorithm
Deterministic algorithm
In computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...
that performs best against that distribution. Thus, to establish a lower bound on the performance of randomized algorithms, it suffices to find an appropriate distribution of difficult inputs, and to prove that no deterministic algorithm can perform well against that distribution. This principle is named after Andrew Yao
Andrew Yao
Andrew Chi-Chih Yao is a prominent computer scientist and computational theorist. Yao used the minimax theorem to prove what is now known as Yao's Principle.Yao was born in Shanghai, China...
, who first proposed it.
Yao's principle may be interpreted in game theoretic
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
terms, via a two-player zero sum game in which one player, Alice
Alice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
, selects a deterministic algorithm, the other player, Bob, selects an input, and the payoff is the cost of the selected algorithm on the selected input. Any randomized algorithm R may be interpreted as a randomized choice among deterministic algorithms, and thus as a strategy for Alice. By von Neumann's
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
minimax theorem, Bob has a randomized strategy that performs at least as well against R as it does against the best pure strategy Alice might choose; that is, Bob's strategy defines a distribution on the inputs such that the expected cost of R on that distribution (and therefore also the worst case expected cost of R) is no better than the expected cost of any single deterministic algorithm against the same distribution.
Statement
Let us state the principle for Las VegasLas Vegas algorithm
In computing, a Las Vegas algorithm is a randomized algorithm that always gives correct results; that is, it always produces the correct result or it informs about the failure. In other words, a Las Vegas algorithm does not gamble with the verity of the result; it gambles only with the resources...
randomized algorithms, i.e., distributions over deterministic algorithms that are correct on every input but have varying costs. It is straightforward to adapt the principle to Monte Carlo
Monte Carlo algorithm
In computing, a Monte Carlo algorithm is a randomized algorithm whose running time is deterministic, but whose output may be incorrect with a certain probability....
algorithms, i.e., distributions over deterministic algorithms that have bounded costs but can be incorrect on some inputs.
Consider a problem over the inputs
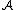, and let be the set of all possible deterministic algorithms that correctly solve the problem.For any algorithm
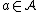and input , let 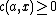be the cost of algorithm run on input .Let
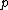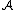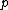be a probability distributions over the algorithms , and let denote a random algorithm chosen according to . Let 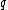be a probability distribution over the inputs 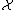, and let 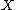denote a random input chosen according to 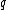. Then,-
,
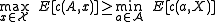i.e., the worst-case expected cost of the randomized algorithm is at least the cost of the best deterministic algorithm against input distribution
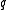.Proof
Let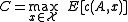. For every input , we have 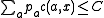. Therefore, 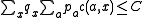. Using Fubini's theoremFubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
, since all terms are non-negative we can switch the order of summation, giving
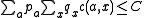. By the Pigeonhole principle, there must exist an algorithm so that 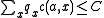, concluding the proof.As mentioned above, this theorem can also be seen as a very special case of the Minimax theorem.
External links
- Favorite theorems: Yao principle, Lance Fortnow, October 16, 2006.