Zsigmondy's theorem
Encyclopedia
In number theory
, Zsigmondy's theorem, named after Karl Zsigmondy
, states that if a > b > 0 are coprime
integer
s, then for any natural number
n > 1 there is a prime number
p (called a primitive prime divisor) that divides an − bn and does not divide ak − bk for any positive integer k < n, with the following exceptions:
This generalized Bang's theorem which states that if n>1 and n is not equal to 6, then 2n-1 has a prime divisor not dividing any 2k-1 with k<n.
Similarly,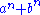
has at least one primitive prime divisor with the exception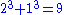 
Zsigmondy's theorem is often useful, especially in group theory, where it is used to prove that various groups have distinct orders except when they are known to be the same
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Zsigmondy's theorem, named after Karl Zsigmondy
Karl Zsigmondy
Karl Zsigmondy was an Austrian mathematician of Hungarian ethnicity. He was a son of Adolf Zsigmondy from Pozsony, Kingdom of Hungary and his mother was Irma von Szakmáry of Martonvásár, Kingdom of Hungary....
, states that if a > b > 0 are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, then for any natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n > 1 there is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p (called a primitive prime divisor) that divides an − bn and does not divide ak − bk for any positive integer k < n, with the following exceptions:
- a = 2, b = 1, and n = 6; or
- a + b is a power of two, and n = 2.
This generalized Bang's theorem which states that if n>1 and n is not equal to 6, then 2n-1 has a prime divisor not dividing any 2k-1 with k<n.
Similarly,
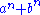has at least one primitive prime divisor with the exception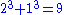 Zsigmondy's theorem is often useful, especially in group theory, where it is used to prove that various groups have distinct orders except when they are known to be the same