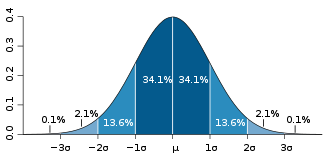
68-95-99.7 rule
Encyclopedia
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the 68-95-99.7 rule, or three-sigma rule, or empirical rule, states that for a normal distribution, nearly all values lie within 3 standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
s of the mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
.
About 68.27% of the values lie within 1 standard deviation of the mean. Similarly, about 95.45% of the values lie within 2 standard deviations of the mean. Nearly all (99.73%) of the values lie within 3 standard deviations of the mean.
In mathematical notation, these facts can be expressed as follows, where x is an observation from a normally distributed random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, μ is the mean of the distribution, and σ is its standard deviation:
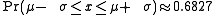
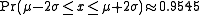
These numerical values come from the cumulative distribution function of the normal distribution. For example, Φ(2) ≈ 0.9772, or Pr(x ≤ μ + 2σ) ≈ 0.9772. Note that this is not a symmetrical interval - this is merely the probability that an observation is less than μ + 2σ. To compute the probability that an observation is within 2 standard deviations of the mean (small differences due to rounding):
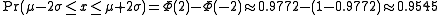
Statisticians might express these intervals as confidence intervals
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
:
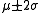is approximately a 95% confidence interval.Uses
This rule is often used to quickly get a rough probability estimate of something, given its standard deviation, if the population is assumed normal, thus also as a simple test for outliers (if the population is assumed normal), and as a normality testNormality test
In statistics, normality tests are used to determine whether a data set is well-modeled by a normal distribution or not, or to compute how likely an underlying random variable is to be normally distributed....
(if the population is potentially not normal).
Recall that to pass from a sample to a number of standard deviations, one
computes the deviation
Deviation (statistics)
In mathematics and statistics, deviation is a measure of difference for interval and ratio variables between the observed value and the mean. The sign of deviation , reports the direction of that difference...
, either the error or residual
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
(accordingly if one knows the population mean or only estimates it), and then either uses standardizing (dividing by the population standard deviation), if the population parameters are known, or studentizing (dividing by an estimate of the standard deviation), if the parameters are unknown and only estimated.
To use as a test for outliers or a normality test, one computes the size of deviations in terms of standard deviations, and compares this to expected frequency. Given a sample set, compute the studentized residual
Studentized residual
In statistics, a studentized residual is the quotient resulting from the division of a residual by an estimate of its standard deviation. Typically the standard deviations of residuals in a sample vary greatly from one data point to another even when the errors all have the same standard...
s and compare these to the expected frequency: points that fall more than 3 standard deviations from the norm are likely outliers (unless the sample size
Sample size
Sample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...
is significantly large, by which point one expects a sample this extreme), and if there are many points more than 3 standard deviations from the norm, one likely has reason to question the assumed normality of the distribution. This holds ever more strongly for moves of 4 or more standard deviations.
One can compute more precisely, approximating the number of extreme moves of a given magnitude or greater by a Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
, but simply, if one has multiple 4 standard deviation moves in a sample of size 1,000, one has strong reason to consider these outliers or question the assumed normality of the distribution.
Higher deviations
Because of the exponential tails of the normal distribution, odds of higher deviations decrease very quickly. From the Rules for normally distributed data:| Range | Population in range | Expected frequency outside range | Approx. frequency for daily event |
|---|---|---|---|
| μ ± 1σ | 1 in 3 | Twice a week | |
| μ ± 1.5σ | 1 in 7 | Weekly | |
| μ ± 2σ | 1 in 22 | Every three weeks | |
| μ ± 2.5σ | 1 in 81 | Every 11.5 weeks | |
| μ ± 3σ | 1 in 370 | Yearly | |
| μ ± 3,5σ | 1 in 2149 | Every 5.9 years | |
| μ ± 4σ | 1 in | Every 43 years (twice in a lifetime) | |
| μ ± 4.5σ | 1 in | Every 403 years | |
| μ ± 5σ | 1 in | Every years (once in recorded history) | |
| μ ± 5.5σ | 1 in | Every years | |
| μ ± 6σ | 1 in | Every 1.388 million years | |
| μ ± 6.5σ | 1 in | Every 34.087 million years | |
| μ ± 7σ | 1 in | Every 1.070 years | |
| μ ± σ | 1 in | Every days |
Thus for a daily process, a 6σ event is expected to happen less than once in a million years. This gives a simple normality test: if one witnesses a 6σ in daily data and significantly fewer than 1 million years have passed, then a normal distribution most likely does not provide a good model for the magnitude or frequency of large deviations in this respect.