
AKLT Model
Encyclopedia
The AKLT model is an extension of the one-dimensional quantum
Heisenberg spin model
. The proposal and exact solution of this model by Affleck, Lieb, Kennedy and Tasaki provided crucial insight into the physics of the spin 1 Heisenberg chain. It has also served as a useful testbed for such concepts as valence bond solid order, topological order
and matrix product state wavefunctions.
. Because two out of every set of three neighboring spins in a Majumdar-Ghosh ground state are paired into a singlet, or valence bond, the three spins together can never be found to be in a spin 3/2 state. In fact, the Majumdar-Ghosh Hamiltonian is nothing but the sum of all projectors of three neighboring spins onto a 3/2 state.
The main insight of the AKLT paper was that this construction could be generalized to obtain exactly solvable models for spin sizes other than 1/2. Just as one end of a valence bond is a spin 1/2, the ends of two valence bonds can be combined into a spin 1, three into a spin 3/2, etc.
For every adjacent pair of the spin 1's, two of the constituent spin 1/2's are stuck in a total spin zero state. Therefore each pair of spin 1's is forbidden from being in a combined spin 2 state. By writing this condition as a sum of projectors, AKLT arrived at the following Hamiltonian
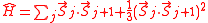
Pictorially, this may be represented as
Here the solid points represent spin 1/2's which are put into singlet states. The lines connecting the spin 1/2's are the valence bonds indicating the pattern of singlets. The ovals are projection operators which "tie" together two spin 1/2's into a single spin 1, projecting out the spin 0 or singlet subspace and keeping only the spin 1 or triplet subspace. The symbols +, 0 and - label the standard spin 1 basis states.. The AKLT model also was solved on lattices of higher dimension, even in quasicrystals. AKLT was also generalized in another direction: the model was constructed for higher Lie
algebras including SU(n).
last spin 1 have only a single neighbor, leaving one of their constituent spin 1/2's unpaired. As a result, the ends of the chain behave like free spin 1/2 moments even though
the physical system consists of spin 1's only.
The spin 1/2 edge states of the AKLT chain can be observed in a few different ways. For short chains, the edge states mix into a singlet or a triplet giving either a unique ground state or a three-fold multiplet of ground states. For longer chains, the edge states decouple exponentially quickly as a function of chain length leading to a ground state manifold that is four-fold degenerate. By using a numerical method such as DMRG to measure the local magnetization along the chain, it is also possible to see the edge states directly and to show that they can be removed by placing actual spin 1/2's at the ends. It has even proved possible to detect spin 1/2 edge states in measurements of a quasi-1D magnetic compound containing a small amount of impurities whose role is to break the chains into finite segments.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
Heisenberg spin model
Heisenberg model
The Heisenberg model can refer to two models in statistical mechanics:*Heisenberg model , a classical nearest neighbour spin model*Heisenberg model , a model where the spins are treated quantum mechanically using Pauli matrices....
. The proposal and exact solution of this model by Affleck, Lieb, Kennedy and Tasaki provided crucial insight into the physics of the spin 1 Heisenberg chain. It has also served as a useful testbed for such concepts as valence bond solid order, topological order
Topological order
In physics, topological order is a new kind of order in a quantum state that is beyond the Landau symmetry-breaking description. It cannot be described by local order parameters and long range correlations...
and matrix product state wavefunctions.
Background
A major motivation for the AKLT model was the Majumdar-Ghosh chainMajumdar-Ghosh Model
The Majumdar-Ghosh model is an extension of the one-dimensional quantum Heisenberg spin model in which an extra interaction is added coupling spins two lattice spacings apart such that second-neighbor coupling half as strong the first. It is therefore a special case of the J1 J2 model...
. Because two out of every set of three neighboring spins in a Majumdar-Ghosh ground state are paired into a singlet, or valence bond, the three spins together can never be found to be in a spin 3/2 state. In fact, the Majumdar-Ghosh Hamiltonian is nothing but the sum of all projectors of three neighboring spins onto a 3/2 state.
The main insight of the AKLT paper was that this construction could be generalized to obtain exactly solvable models for spin sizes other than 1/2. Just as one end of a valence bond is a spin 1/2, the ends of two valence bonds can be combined into a spin 1, three into a spin 3/2, etc.
Definition
Affleck et al. were interested in constructing a one-dimensional state with a valence bond between every pair of sites. Because this leads to two spin 1/2's for every site, the result must be the wavefunction of a spin 1 system.For every adjacent pair of the spin 1's, two of the constituent spin 1/2's are stuck in a total spin zero state. Therefore each pair of spin 1's is forbidden from being in a combined spin 2 state. By writing this condition as a sum of projectors, AKLT arrived at the following Hamiltonian
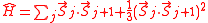
Ground State
By construction, the ground state of the AKLT Hamiltonian is the valence bond solid with a single valence bond connecting every neighboring pair of sites.Pictorially, this may be represented as
Here the solid points represent spin 1/2's which are put into singlet states. The lines connecting the spin 1/2's are the valence bonds indicating the pattern of singlets. The ovals are projection operators which "tie" together two spin 1/2's into a single spin 1, projecting out the spin 0 or singlet subspace and keeping only the spin 1 or triplet subspace. The symbols +, 0 and - label the standard spin 1 basis states.. The AKLT model also was solved on lattices of higher dimension, even in quasicrystals. AKLT was also generalized in another direction: the model was constructed for higher Lie
algebras including SU(n).
Spin 1/2 Edge States
For the case of spins arranged in a ring (periodic boundary conditions) the AKLT construction yields a unique ground state. But for the case of an open chain, the first andlast spin 1 have only a single neighbor, leaving one of their constituent spin 1/2's unpaired. As a result, the ends of the chain behave like free spin 1/2 moments even though
the physical system consists of spin 1's only.
The spin 1/2 edge states of the AKLT chain can be observed in a few different ways. For short chains, the edge states mix into a singlet or a triplet giving either a unique ground state or a three-fold multiplet of ground states. For longer chains, the edge states decouple exponentially quickly as a function of chain length leading to a ground state manifold that is four-fold degenerate. By using a numerical method such as DMRG to measure the local magnetization along the chain, it is also possible to see the edge states directly and to show that they can be removed by placing actual spin 1/2's at the ends. It has even proved possible to detect spin 1/2 edge states in measurements of a quasi-1D magnetic compound containing a small amount of impurities whose role is to break the chains into finite segments.

