
Abel's theorem
Encyclopedia
In mathematics
, Abel's theorem for power series relates a limit
of a power series to the sum of its coefficient
s. It is named after Norwegian mathematician Niels Henrik Abel
.
s and let

be the power series with coefficients a. Suppose that the series
 converges. Then
converges. Then

where the variable z is supposed to be real, or, more generally, to lie within any Stoltz angle, that is, a region of the open unit disk where
for some M. Without this restriction, the limit may fail to exist.
Note that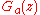 is continuous on the real closed interval [0, t] for t < 1, by virtue of the uniform convergence of the series on compact subsets of the disk of convergence. Abel's theorem allows us to say more, namely that
is continuous on the real closed interval [0, t] for t < 1, by virtue of the uniform convergence of the series on compact subsets of the disk of convergence. Abel's theorem allows us to say more, namely that 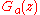 is continuous on [0, 1].
is continuous on [0, 1].
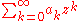 converges, then it follows that
converges, then it follows that
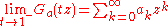
in which the limit is taken from below
.
, R, of the power series is equal to 1 and we cannot be sure whether the limit should be finite or not. See e.g. the binomial series
. Abel's theorem allows us to evaluate many series in closed form. For example, when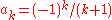 , we obtain
, we obtain 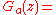 ln
ln for
for 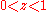 , by integrating the uniformly convergent geometric power series term by term on [-z, 0]; thus the series
, by integrating the uniformly convergent geometric power series term by term on [-z, 0]; thus the series 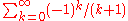 converges to ln(2) by Abel's theorem. Similarly,
converges to ln(2) by Abel's theorem. Similarly, 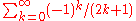 converges to arctan(1) =
converges to arctan(1) = 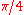 .
.
Ga(z) is called the generating function
of the sequence a. Abel's theorem is frequently useful in dealing with generating functions of real-valued and non-negative sequence
s, such as probability-generating function
s. In particular, it is useful in the theory of Galton–Watson processes.
 , we may assume that
, we may assume that 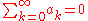 . Let
. Let  . Then substituting
. Then substituting 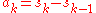 and performing a simple manipulation of the series results in
and performing a simple manipulation of the series results in
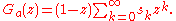
Given , pick n large enough so that
, pick n large enough so that 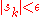 for all
for all  and note that
and note that
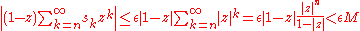
when z lies within the given Stoltz angle. Whenever z is sufficiently close to 1 we have

so that when z is both sufficiently close to 1 and within the Stoltz angle.
when z is both sufficiently close to 1 and within the Stoltz angle.
, and their summation methods, contains many theorems of abelian type and of tauberian type.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Abel's theorem for power series relates a limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
of a power series to the sum of its coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s. It is named after Norwegian mathematician Niels Henrik Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
.
Theorem
Let a = {ak: k ≥ 0} be any sequence of real or complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s and let

be the power series with coefficients a. Suppose that the series
 converges. Then
converges. Then
where the variable z is supposed to be real, or, more generally, to lie within any Stoltz angle, that is, a region of the open unit disk where
for some M. Without this restriction, the limit may fail to exist.
Note that
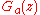 is continuous on the real closed interval [0, t] for t < 1, by virtue of the uniform convergence of the series on compact subsets of the disk of convergence. Abel's theorem allows us to say more, namely that
is continuous on the real closed interval [0, t] for t < 1, by virtue of the uniform convergence of the series on compact subsets of the disk of convergence. Abel's theorem allows us to say more, namely that 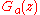 is continuous on [0, 1].
is continuous on [0, 1].Remark
As an immediate consequence of this theorem, if z is any nonzero complex number for which the series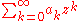 converges, then it follows that
converges, then it follows that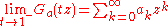
in which the limit is taken from below
One-sided limit
In calculus, a one-sided limit is either of the two limits of a function f of a real variable x as x approaches a specified point either from below or from above...
.
Applications
The utility of Abel's theorem is that it allows us to find the limit of a power series as its argument (i.e. z) approaches 1 from below, even in cases where the radius of convergenceRadius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
, R, of the power series is equal to 1 and we cannot be sure whether the limit should be finite or not. See e.g. the binomial series
Binomial series
In mathematics, the binomial series is the Taylor series at x = 0 of the function f given by f = α, where is an arbitrary complex number...
. Abel's theorem allows us to evaluate many series in closed form. For example, when
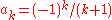 , we obtain
, we obtain 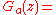 ln
ln for
for 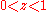 , by integrating the uniformly convergent geometric power series term by term on [-z, 0]; thus the series
, by integrating the uniformly convergent geometric power series term by term on [-z, 0]; thus the series 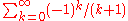 converges to ln(2) by Abel's theorem. Similarly,
converges to ln(2) by Abel's theorem. Similarly, 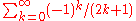 converges to arctan(1) =
converges to arctan(1) = 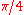 .
.Ga(z) is called the generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
of the sequence a. Abel's theorem is frequently useful in dealing with generating functions of real-valued and non-negative sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s, such as probability-generating function
Probability-generating function
In probability theory, the probability-generating function of a discrete random variable is a power series representation of the probability mass function of the random variable...
s. In particular, it is useful in the theory of Galton–Watson processes.
Outline of proof
After subtracting a constant from , we may assume that
, we may assume that 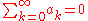 . Let
. Let  . Then substituting
. Then substituting 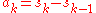 and performing a simple manipulation of the series results in
and performing a simple manipulation of the series results in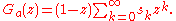
Given
 , pick n large enough so that
, pick n large enough so that 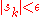 for all
for all  and note that
and note that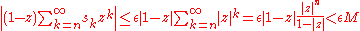
when z lies within the given Stoltz angle. Whenever z is sufficiently close to 1 we have

so that
 when z is both sufficiently close to 1 and within the Stoltz angle.
when z is both sufficiently close to 1 and within the Stoltz angle.Related concepts
Converses to a theorem like Abel's are called Tauberian theorems: there is no exact converse, but results conditional on some hypothesis. The field of divergent seriesDivergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
, and their summation methods, contains many theorems of abelian type and of tauberian type.


