
Abundant number
Encyclopedia
In number theory
, an abundant number or excessive number is a number n for which the sum of divisors σ(n)>2n, or, equivalently, the sum of proper divisors (or aliquot sum) s(n)>n. The value σ(n)-2n (or s(n)-n) is known as the abundance.
For example, the divisors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24, whose sum is 60. Because 60 is more than 2 × 24, the number 24 is abundant. Its abundance is 60 − (2 × 24) = 12.
s, or numbers the sum of whose proper factors is less than the number itself (or σ(n) < 2n.) The natural number
s were first classified as either deficient, perfect or abundant by Nicomachus
in his Introductio Arithmetica
(circa 100) who described abundant numbers as like deformed animals with too many limbs.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, an abundant number or excessive number is a number n for which the sum of divisors σ(n)>2n, or, equivalently, the sum of proper divisors (or aliquot sum) s(n)>n. The value σ(n)-2n (or s(n)-n) is known as the abundance.
Examples
The first few abundant numbers are:- 12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100, 102, … .
For example, the divisors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24, whose sum is 60. Because 60 is more than 2 × 24, the number 24 is abundant. Its abundance is 60 − (2 × 24) = 12.
Properties
- The smallest odd abundant number is 945
- The smallest not divisible by 2 or by 3 is 5391411025 whose prime factors are 5, 7, 11, 13, 17, 19, 23, and 29. An algorithm given by Iannucci in 2005 shows how to find the smallest abundant number not divisible by the first k primes. If
 represents the smallest abundant number not divisible by the first k primes then for all
represents the smallest abundant number not divisible by the first k primes then for all 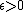 we have:
we have: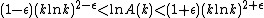 for k sufficiently large.
for k sufficiently large.
- Infinitely many even and oddEven and odd numbersIn mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
abundant numbers exist. Marc Deléglise showed in 1998 that the natural densityNatural densityIn number theory, asymptotic density is one of the possibilities to measure how large a subset of the set of natural numbers is....
of the set of abundant numbers and perfect numbers is between 0.2474 and 0.2480.
- Every proper multiple of a perfect numberPerfect numberIn number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
, and every multiple of an abundant number, is abundant.
- Every integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
greater than 20161 can be written as the sum of two abundant numbers..
- An abundant number which is not a semiperfect numberSemiperfect numberIn number theory, a semiperfect number or pseudoperfect number is a natural number n that is equal to the sum of all or some of its proper divisors. A semiperfect number that is equal to the sum of all its proper divisors is a perfect number....
is called a weird numberWeird numberIn number theory, a weird number is a natural number that is abundant but not semiperfect.In other words, the sum of the proper divisors of the number is greater than the number, but no subset of those divisors sums to the number itself.- Examples :The smallest weird number is 70...
; an abundant number with abundance 1 is called a quasiperfect numberQuasiperfect numberIn mathematics, a quasiperfect number is a theoretical natural number n for which the sum of all its divisors is equal to 2n + 1...
, however, none have yet been found.
Related concepts
Closely related to abundant numbers are perfect numbers, that is numbers the sum of whose proper factors equals the number itself (such as 6 and 28) (or more formally, σ(n) = 2n), and deficient numberDeficient number
In number theory, a deficient number or defective number is a number n for which the sum of divisors σIn number theory, a deficient number or defective number is a number n for which the sum of divisors σIn number theory, a deficient number or defective number is a number n for which...
s, or numbers the sum of whose proper factors is less than the number itself (or σ(n) < 2n.) The natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s were first classified as either deficient, perfect or abundant by Nicomachus
Nicomachus
Nicomachus was an important mathematician in the ancient world and is best known for his works Introduction to Arithmetic and Manual of Harmonics in Greek. He was born in Gerasa, in the Roman province of Syria , and was strongly influenced by Aristotle...
in his Introductio Arithmetica
Introduction to Arithmetic
Introduction to Arithmetic was written by Nicomachus almost two thousand years ago, and contains both philosophical prose and very basic mathematical ideas. Nicomachus refers to Plato quite often, and wrote about how philosophy can only be possible if one knows enough about mathematics. This is...
(circa 100) who described abundant numbers as like deformed animals with too many limbs.

